题目内容
2.已知函数f(x)=ax+$\frac{x-2}{x+1}$(a>1),判断f(x)=0的根的个数.分析 f(x)=0是否有根,即看函数y=ax和y=-$\frac{x-2}{x+1}$交点的个数,所以通过画图即可得出结论.
解答 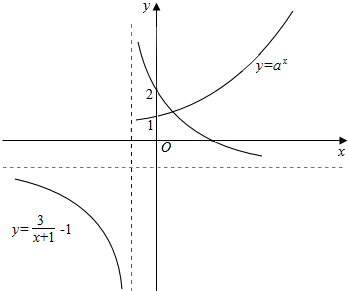 解:$\frac{x-2}{x+1}$=1-$\frac{3}{x+1}$,
解:$\frac{x-2}{x+1}$=1-$\frac{3}{x+1}$,
∴由f(x)=0得,ax=$\frac{3}{x+1}$-1,
∴函数y=ax与y=$\frac{3}{x+1}$-1图象交点的横坐标即是上面方程的解,
而y=$\frac{3}{x+1}$-1图象是由y=$\frac{3}{x}$的图象
沿x轴向左平移一个单位,向上平移一个单位得到,所以图象如下所示:
由图象可看出y=ax与y=$\frac{3}{x+1}$-1
图象交点的横坐标大于0;
即方程f(x)=0的根的个数为1.
点评 本题考查指数函数的单调性,以及指数函数的图象,反比例函数的图象,图象平移的知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.设U=Z,M={x|x=2k,k∈Z},P={x|x=3k,k∈Z},则M∩(CUP)=( )
| A. | {x|x=3k±1,k∈Z} | B. | {x|x=4k±1,k∈Z} | C. | {x|x=6k±2,k∈Z} | D. | {x|x=4k或4k+2,k∈Z} |
12.设集合A{x||x-5|≤6,x∈N*},集合B={x|x2-x-12<0},则A∩B=( )
| A. | [-1,4) | B. | [-1,4) | C. | {0,1,2,3} | D. | {1,2,3} |