题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为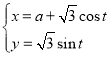 (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(异于极点),若
上(异于极点),若![]() 四点依次在同一条直线
四点依次在同一条直线![]() 上,且
上,且![]() 成等比数列,求
成等比数列,求![]() 的极坐标方程.
的极坐标方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先根据平方关系消元得曲线![]() 的直角坐标方程,再根据
的直角坐标方程,再根据![]() 将直角坐标方程化为极坐标方程,最后代入
将直角坐标方程化为极坐标方程,最后代入![]() 点极坐标,可求出
点极坐标,可求出![]() 的值,进而得出答案;
的值,进而得出答案;
(2)先设直线![]() 的极坐标方程为
的极坐标方程为![]() ,代入
,代入![]() ,根据
,根据![]() 成等比数列得
成等比数列得![]() ,代入化简可得
,代入化简可得![]() ,进而可得出答案.
,进而可得出答案.
(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,化简得
,化简得![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() .
.
代入点![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() ,所以曲线
,所以曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)由题意,可设直线![]() 的极坐标方程为
的极坐标方程为![]() ,设点
,设点![]() ,则
,则![]() .
.
联立 ,得
,得![]() ,所以
,所以![]() ,
,![]() .
.
联立![]() ,得
,得![]() .
.
因为![]() 成等比数列,所以
成等比数列,所以![]() ,即
,即![]() .
.
所以![]() ,解得
,解得![]() .
.
所以![]() 的极坐标方程为
的极坐标方程为![]() 或
或![]() .
.

【题目】某县一中学的同学为了解本县成年人的交通安全意识情况,利用假期进行了一次全县成年人安全知识抽样调查.已知该县成年人中![]() 的拥有驾驶证,先根据是否拥有驾驶证,用分层抽样的方法抽取了100名成年人,然后对这100人进行问卷调查,所得分数的频率分布直方图如下图所示.规定分数在80以上(含80)的为“安全意识优秀”.
的拥有驾驶证,先根据是否拥有驾驶证,用分层抽样的方法抽取了100名成年人,然后对这100人进行问卷调查,所得分数的频率分布直方图如下图所示.规定分数在80以上(含80)的为“安全意识优秀”.
拥有驾驶证 | 没有驾驶证 | 合计 | |
得分优秀 | |||
得分不优秀 | 25 | ||
合计 | 100 |

(1)补全上面![]() 的列联表,并判断能否有超过
的列联表,并判断能否有超过![]() 的把握认为“安全意识优秀与是否拥有驾驶证”有关?
的把握认为“安全意识优秀与是否拥有驾驶证”有关?
(2)若规定参加调查的100人中分数在70以上(含70)的为“安全意识优良”,从参加调查的100人中根据安全意识是否优良,按分层抽样的方法抽出5人,再从5人中随机抽取3人,试求抽取的3人中恰有一人为“安全意识优良”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

