��Ŀ����
����Ŀ����ij������һ�������ȡij�ֲ�Ʒ50������Ʒ�ߴ磨��λ��cm�����ڸ���С���Ƶ���ֲ����±���
���ݷ��� | [12.5��15.5�� | [15.5��18.5�� | [18.5��21.5�� | [21.5��24.5�� | [24.5��27.5�� | [27.5��30.5�� | [30.5��33.5�� |
Ƶ�� | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
��1������Ƶ���ֲ�������ò�Ʒ�ߴ�����[27.5��33.5]�ڵĸ��ʣ�
��2������50����Ʒ�ߴ������ƽ����![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
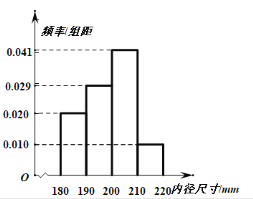
��3������Ƶ���ֲ���Ӧ��ֱ��ͼ��������Ϊ���ֲ�Ʒ�ߴ�![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ����ƽ��ֵ
����Ϊ����ƽ��ֵ![]() ��
��![]() ������������
������������![]() ���������
���������![]() .���ø���̬�ֲ�����
.���ø���̬�ֲ�����![]() ��
��![]() ��.
��.
������1�����������![]() ������̬�ֲ�
������̬�ֲ�![]() ����
����![]()
![]() ����2��
����2��![]() .
.
���𰸡���1��0.16����2��22.7����3��0.1587
��������
��1��ֱ�Ӹ���Ƶ���ֲ�����ߴ�����[27.5��33.5���ڵĸ��ʣ�
��2����ÿһ�����ݵ��м�ֵ����Ƶ�������������ƽ������
��3��������![]() �����
�����![]() ��
��![]() ��������̬�ֲ����ߵĶԳ�����P��z��27.43����0.1587��
��������̬�ֲ����ߵĶԳ�����P��z��27.43����0.1587��
��1������Ƶ���ֲ�����֪����Ʒ�ߴ�����[27.5,33.5]�ڵĸ���Ϊ![]() ��
��
��2������ƽ����![]()
![]() ��
��
��3��������![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]() ��
��![]() .
.

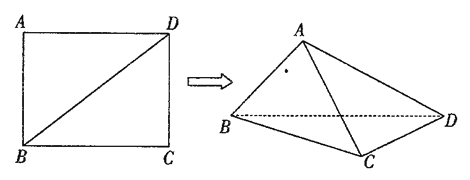
 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�����Ŀ��ij��ҵΪȷ����һ��Ͷ��ij�ֲ�Ʒ���з����ã����˽����з�����![]() ����λ��ǧ��Ԫ������������
����λ��ǧ��Ԫ������������![]() ����λ��ǧ�������Ӱ�죬ͳ���˽�
����λ��ǧ�������Ӱ�죬ͳ���˽�![]() ��Ͷ������з�����
��Ͷ������з�����![]() ����������
����������![]() �����ݣ��õ�ɢ��ͼ��ͼ��ʾ��
�����ݣ��õ�ɢ��ͼ��ͼ��ʾ��
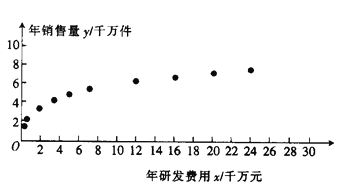
(1)����ɢ��ͼ�ж�![]() ��
��![]() ������
������![]() ������
��Ϊ����![]() �ij�������һ�����ʺ���Ϊ��������
�ij�������һ�����ʺ���Ϊ��������![]() �����з�����
�����з�����![]() �Ļع鷽�����ͣ�ֻҪ�����жϼ��ɣ�����˵�����ɣ�
�Ļع鷽�����ͣ�ֻҪ�����жϼ��ɣ�����˵�����ɣ�
(2)�������������´�������![]() ���õ����ͳ������ֵ���±������ݵ�(1)�ʵ��жϽ�����������ݣ���
���õ����ͳ������ֵ���±������ݵ�(1)�ʵ��жϽ�����������ݣ���![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
|
|
|
|
15 | 15 | 28.25 | 56.5 |
(3)��֪��ҵ������![]() ����λ��ǧ��Ԫ����
����λ��ǧ��Ԫ�����Ĺ�ϵΪ
![]() ������
������![]() �������ݵ�(2)�ʵĽ���жϣ�Ҫʹ�ø���ҵ��һ������������Ԥ����һ��ӦͶ������з�����?
�������ݵ�(2)�ʵĽ���жϣ�Ҫʹ�ø���ҵ��һ������������Ԥ����һ��ӦͶ������з�����?
��������һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ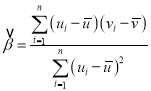 ��
��![]()