题目内容
5．已知函数f（x）=x2-2，其中x∈[0，2]，这个函数的最大值和最小值分别为（ ）| A． | -2和1 | B． | 2和-2 | C． | 2和-1 | D． | -1和2 |
分析 根据图象特征，求出函数的最大值和最小值，得到本题结论
解答 解：∵f（x）=x2-2，x∈[0，2]，
∴当x=0时，f（x）有最小值-2，
当x=2时，f（x）有最大值2，
故选：B．
点评 本题考查了二次函数在区间上的值域，难度不大，属于基础题．
练习册系列答案
相关题目
20．己知直线l1与l2均过点M（4，2），且l1⊥l2，l1与2分别和x，y轴交于A，B两点，点P是线段AB的中点，则|OP|的最小值是（ ）
| A． | 2 | B． | 5 | C． | $\sqrt{5}$ | D． | $\frac{\sqrt{13}}{2}$ |
10．函数f（x）=23-x在区间（-∞，0）上的单调性是（ ）
| A． | 增函数 | B． | 减函数 | ||
| C． | 常数 | D． | 有时是增函数有时是减函数 |
17．函数f（x）=x2-2（a-1）x+1在区间[5，+∞）上是增函数，则实数a的取值范围是（ ）
| A． | [6，+∞） | B． | （6，+∞） | C． | （-∞，6] | D． | （-∞，6） |
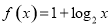与
在同一直角坐标系下的图象大致是（ ）
B．
D．