题目内容
14.赵州桥圆拱的跨度是37.4m,圆拱高约为7.2m,适当选取坐标系求出其圆拱所在圆的方程.分析 以圆心为原点,以圆拱高所在直线为y轴建立坐标系,利用勾股定理求出圆的半径,即可求出圆拱所在圆的方程.
解答  解:以圆心为原点,以圆拱高所在直线为y轴建立坐标系.
解:以圆心为原点,以圆拱高所在直线为y轴建立坐标系.
设圆的半径为R.
由题意,|AD|=37.4m,|CD|=7.2m,|AC|=$\frac{1}{2}$|AD|=18.7m
在Rt△ACO中,R2=18.72+(R-7.2)2,解得R=27.9m
所求圆的方程为x2+y2=27.92
点评 本题考查圆的方程,考查学生的计算能力,正确建立坐标系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知函数f(x)=x2-2,其中x∈[0,2],这个函数的最大值和最小值分别为( )
| A. | -2和1 | B. | 2和-2 | C. | 2和-1 | D. | -1和2 |
9.判断下列对应关系是否为函数,若不是,说明理由:
(1)x→$\frac{2}{x}$,x∈R;
(2)x→y,y2=x,x∈N,y∈R;
(3)y=$\sqrt{x-2}$+$\sqrt{1-x}$.
(1)x→$\frac{2}{x}$,x∈R;
(2)x→y,y2=x,x∈N,y∈R;
(3)y=$\sqrt{x-2}$+$\sqrt{1-x}$.
 函数
函数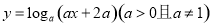 的图象必过定点
的图象必过定点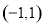 ;命题
;命题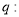 如果函数
如果函数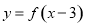 的图象关于原点对称,那么函数
的图象关于原点对称,那么函数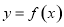 的图象关于点
的图象关于点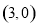 对称,则命题
对称,则命题 为__________(填“真”或“假”).
为__________(填“真”或“假”). ,山区边界曲线为
,山区边界曲线为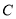 .计划修建的公路为
.计划修建的公路为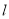 ,如图所示,
,如图所示,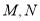 为
为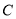 的两个端点,测得点
的两个端点,测得点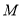 到
到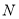 到
到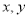 轴,建立平面直角坐标系
轴,建立平面直角坐标系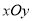 .假设曲线
.假设曲线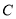 符合函数
符合函数 (其中
(其中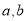 为常数)模型.
为常数)模型.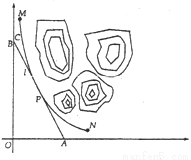
 的值;
的值;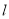 与曲线
与曲线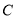 相切于
相切于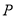 点,
点, 的横坐标为
的横坐标为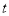 .
.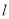 长度的函数解析式
长度的函数解析式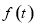 ,并写出其定义域;
,并写出其定义域; 为何值时,公路
为何值时,公路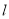 的长度最短?求出最短长度.
的长度最短?求出最短长度.