题目内容
【题目】在等比数列{an}中，a2=6，a2+a3=24，在等差数列{bn}中，b1=a1 ， b3=﹣10．
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Sn ．
【答案】
（1）解：设等比数列{an}的公比为q，由a2=6，a2+a3=26，可得 6+6q=24，解得q=3，
∴a1=2，an=2×3n﹣1．
（2）解：b1=a1=2b1=a1=2，b3=﹣10，又{bn}数列{bn}是等差数列，∴b3﹣b1=2d=﹣12，解得d=﹣6．
∴ 
，
∴数列{bn}的前n项和Sn为﹣3n2+5n．
【解析】（1）利用等比数列的通项公式即可得出；（2）利用等差数列的通项公式及其求和公式即可得出．
【考点精析】通过灵活运用等比数列的通项公式（及其变式）和等比数列的前n项和公式，掌握通项公式：
；前
项和公式：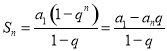
即可以解答此题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（万元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求：
（1）求
； （2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算a,b的值时,可根据以下公式：
