题目内容
(本小题共12分)已知由正数组成的数列{an}的前n项和为Sn=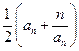 ,
,
①求S1,S2,S3;
②猜想Sn的表达式,并用数学归纳法证明你的结论;
③求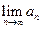
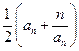 ,
,①求S1,S2,S3;

②猜想Sn的表达式,并用数学归纳法证明你的结论;
③求
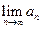
①S1=1,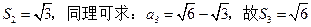
②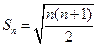 ,证明略
,证明略
③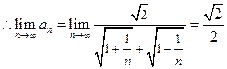
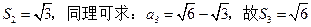
②
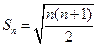 ,证明略
,证明略③
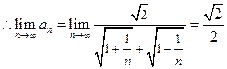
解:⑴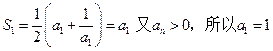 (1分)
(1分)
即S1=1, 又
 (2分)
(2分)
故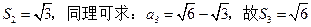 (3分)
(3分)
⑵猜想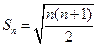 ,下面用数学归纳法证明: (4分)
,下面用数学归纳法证明: (4分)
①当n=1,2,3时,结论成立。
②假设当n=k(k≥3,k∈N*)时结论成立,则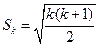 (6分)
(6分)
则当n=k+1时
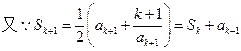
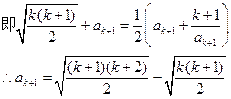
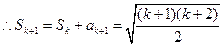
故当n=k+1时,结论成立。
综上①②得:对任意正整数n猜想均成立。 (9分)
③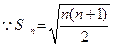 ,所以当n≥2时,
,所以当n≥2时,
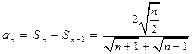
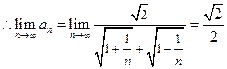 (12分)
(12分)
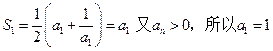 (1分)
(1分)即S1=1, 又

 (2分)
(2分)故
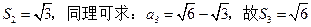 (3分)
(3分)⑵猜想
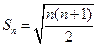 ,下面用数学归纳法证明: (4分)
,下面用数学归纳法证明: (4分)①当n=1,2,3时,结论成立。
②假设当n=k(k≥3,k∈N*)时结论成立,则
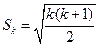 (6分)
(6分)则当n=k+1时
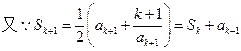
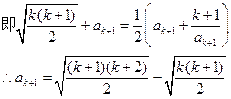
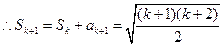
故当n=k+1时,结论成立。
综上①②得:对任意正整数n猜想均成立。 (9分)
③
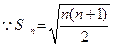 ,所以当n≥2时,
,所以当n≥2时,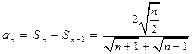
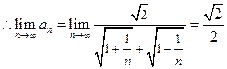 (12分)
(12分)
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
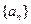 中,
中,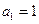 ,且
,且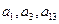 成等比数列.
成等比数列. 
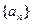 的通项公式;
的通项公式;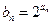 ,求数列
,求数列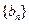 的前
的前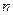 项和
项和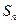 .
.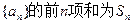 ,
,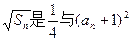 的等比中项。
的等比中项。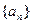 是等差数列;(2)若
是等差数列;(2)若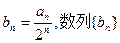 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。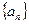 的前
的前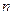 项和为
项和为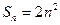 ,
,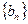 为等比数列,且
为等比数列,且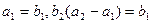 .
.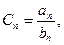 求数列
求数列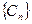 的前n项和
的前n项和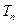 。
。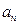 }中,
}中,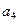 =14,前10项和
=14,前10项和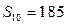 .
.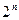 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前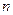 项和
项和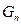 .
.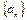 满足
满足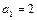 ,
,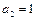 ,且
,且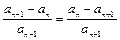 (
(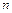 ≥2),则这个数列的第10项等于
≥2),则这个数列的第10项等于



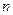 项的和为
项的和为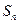 ,若
,若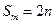 ,
,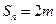 ,(
,(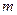 、
、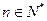 且
且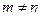 ),则公差
),则公差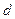 的值是( )
的值是( ) 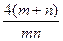
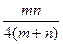
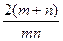
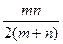
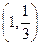 是函数
是函数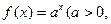 且
且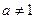 )的图象上一点,等比数列
)的图象上一点,等比数列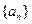 的前
的前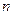 项和为
项和为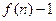 ,数列
,数列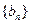
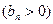 的首项为
的首项为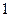 ,且前
,且前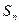 满足
满足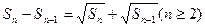
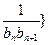 前
前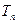 ,问
,问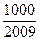 的最小正整数
的最小正整数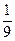 ,则a36= .
,则a36= .