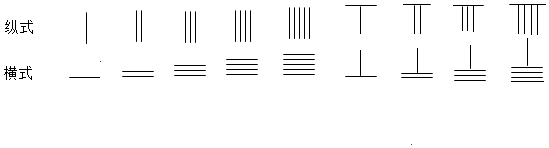
题目内容
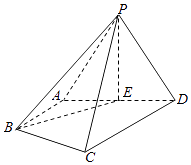
【题目】如图,在梯形ABCD中,AB∥CD, ![]() ,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.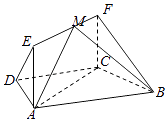
(1)求证:EF⊥平面BCF;
(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.
【答案】
(1)解:在梯形ABCD中,∵AB∥CD,AD=CD=BC=1,
又∵ ![]() ,∴AB=2,∴AC2=AB2+BC2﹣2ABBCcos60°=3.…∴AB2=AC2+BC2.∴BC⊥AC.…
,∴AB=2,∴AC2=AB2+BC2﹣2ABBCcos60°=3.…∴AB2=AC2+BC2.∴BC⊥AC.…
∵CF⊥平面ABCD,AC平面ABCD,∴AC⊥CF,… 而CF∩BC=C,∴AC⊥平面BCF.…
∵EF∥AC,∴EF⊥平面BCF.…
(2)由(1)可建立分别以直线CA,CB,CF为x轴,y轴,z轴的如图所示建立空间直角坐标系,
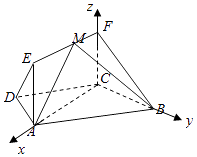
令FM=λ( ![]() ),则C(0,0,0),A(
),则C(0,0,0),A( ![]() ,0,0),B(0,1,0),M(λ,0,1),…
,0,0),B(0,1,0),M(λ,0,1),…
∴ ![]() =(﹣
=(﹣ ![]() ,1,0),
,1,0), ![]() =(λ,﹣1,1),
=(λ,﹣1,1),
设 ![]() 为平面MAB的一个法向量,
为平面MAB的一个法向量,
由 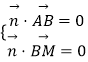 得
得 ![]() 取x=1,则
取x=1,则 ![]() =(1,
=(1, ![]() ,
, ![]() ),…
),…
∵ ![]() =(1,0,0)是平面FCB的一个法向量,
=(1,0,0)是平面FCB的一个法向量,
∴ 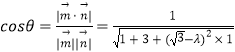 =
= ![]() .
.
∵ ![]() ,∴当λ=0时,cosθ有最小值
,∴当λ=0时,cosθ有最小值 ![]() ,…
,…
∴点M与点F重合时,平面MAB与平面FCB所成二面角最大,此时二面角的余弦值为 ![]() .
.
【解析】1、由题意可得AB=2,∴AC2=AB2+BC2﹣2ABBCcos60°=3.∴AB2=AC2+BC2.∴BC⊥AC.根据线面垂直的判定定理可得EF⊥平面BCF2;
2、建立空间直角坐标系由向量可得c o s θ=![]() =
=![]() ,∵
,∵ ![]() ,∴当λ=0时,cosθ有最小值
,∴当λ=0时,cosθ有最小值 ![]() ,点M与点F重合时,平面MAB与平面FCB所成二面角最大,此时二面角的余弦值为
,点M与点F重合时,平面MAB与平面FCB所成二面角最大,此时二面角的余弦值为 ![]() .
.

【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.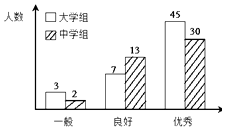
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:K2 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(k2≥k0) | 0.10 | 0.05 | 0.005 |
k0 | 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程 ![]() ;
;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y﹣0.05x2﹣1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 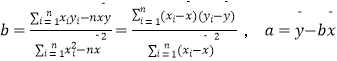 )
)
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() (1)=
(1)= ![]() +1.1,方程乙:
+1.1,方程乙: ![]() (2)=
(2)= ![]() +1.6.
+1.6.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() =yi﹣
=yi﹣ ![]() ,
, ![]() 称为相应于点(xi , yi)的残差(也叫随机误差);
称为相应于点(xi , yi)的残差(也叫随机误差);
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | ﹣0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和Q1及Q2 , 并通过比较Q1 , Q2的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入﹣成本).