题目内容
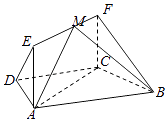
【题目】在四棱锥P﹣ABCD中,△PAD为正三角形,平面PAD⊥平面ABCD,E为AD的中点,AB∥CD,AB⊥AD,CD=2AB=2AD=4.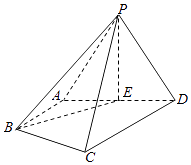
(Ⅰ)求证:平面PCD⊥平面PAD;
(Ⅱ)求直线PB与平面PCD所成角的正弦值;
(Ⅲ)在棱CD上是否存在点M,使得AM⊥平面PBE?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】证明:(Ⅰ)∵△PAD为正三角形,E为AD的中点,∴PE⊥AD.
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,∴PE⊥平面ABCD.
∵CD平面ABCD,∴PE⊥CD.
∵AB∥CD,AB⊥AD,∴CD⊥AD.
∵PE∩AD=E,∴CD⊥平面PAD.
∵CD平面ABCD,
∴平面PCD⊥平面PAD.…
解:(Ⅱ)在平面ABCD内作直线EF⊥AD.
∴EF⊥平面PAD,∴EF⊥PE.
以E为原点建立空间直角坐标系E﹣xyz,如图所示.
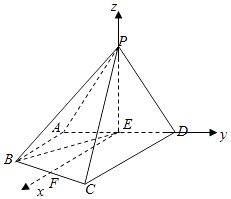
则P(0,0, ![]() ),A(0,﹣1,0),B(2,﹣1,0),C(4,1,0),D(0,1,0).
),A(0,﹣1,0),B(2,﹣1,0),C(4,1,0),D(0,1,0).
![]() =(2,﹣1,﹣
=(2,﹣1,﹣ ![]() ),
), ![]() =(4,1,﹣
=(4,1,﹣ ![]() ),
), ![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
),
设平面PCD的法向量为 ![]() =(x,y,z).
=(x,y,z).
∴ 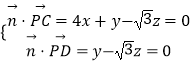 ,令z=
,令z= ![]() ,则
,则 ![]() =(0,3,
=(0,3, ![]() ),
),
设直线PB与平面PCD所成的角为α.
则sinα=|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() .
.
∴直线PB与平面PCD所成角的正弦值为 ![]() .…
.…
(Ⅲ)在棱CD上假设存在点M,使得AM⊥平面PBE.
∵PE⊥平面ABCD,∴PE⊥AM.
要使AM⊥平面PBE成立,只需AM⊥EB成立.
设M(x0,y0,z0), ![]() .λ∈[0,1]
.λ∈[0,1]
∴ ![]() ,即(x,y﹣1,z)=λ(4,0,0).∴x=4λ,y=1,z=0.∴M(4λ,1,0).
,即(x,y﹣1,z)=λ(4,0,0).∴x=4λ,y=1,z=0.∴M(4λ,1,0).
∵ ![]() ,
,
∴由 ![]() ⊥
⊥ ![]() ,得
,得 ![]() =0,即8λ﹣2=0.解得
=0,即8λ﹣2=0.解得 ![]() ∈[0,1].
∈[0,1].
故 ![]() .…
.…
【解析】1、由面面垂直得到线面垂直,再由线线垂直得到平面PCD⊥平面PAD.
2、线面角指的是这条直线在这个平面内的射影和该线所成的角。原点建立空间直角坐标系E﹣xyz,由题意可得
设直线PB与平面PCD所成的角为α.则sinα=|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() .直线PB与平面PCD所成角的正弦值为
.直线PB与平面PCD所成角的正弦值为 ![]() .
.
3、在棱CD上假设存在点M,使得AM⊥平面PBE.∵PE⊥平面ABCD,∴PE⊥AM.要使AM⊥平面PBE成立,只需AM⊥EB成立.由向量知识可得由 ![]() ,
,![]() ,
,![]() 得
得![]() 即8λ﹣2=0.解得 λ = 1 4 ∈[0,1].故
即8λ﹣2=0.解得 λ = 1 4 ∈[0,1].故 ![]() .…
.…