Question

【题目】在平面直角坐标系 中，点 在抛物线 上.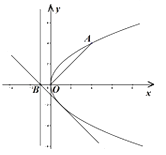

（1）求 的方程和 的焦点的坐标；
（2）设点 为准线与 轴的交点，直线 过点 ，且与直线 垂直，求证： 与 相切.

Answer 1

【答案】
（1）解：因为点 在抛物线 上，
所以 ，解得 .
所以抛物线 的方程为 ，焦点 的坐标
（2）解：准线： 与 轴的交点 ，
直线 的斜率 ，
所以直线 的方程： ，即 ，
由方程组 ，可得 ，
因为 ，所以 与 相切.
【解析】(1)把点的坐标代入到抛物线的方程中求出p的值进而得到抛物线以及焦点坐标。(2)根据点斜式求出直线的方程再联立其与抛物线的方程消元得到关于y的一元二次方程，判断其Δ=0进而得到 l 与 C 相切。