题目内容
13．在△ABC中，D为BC边的中点，H为AD的中点，过点H作一直线MN分别交AB、AC于点M、N，若$\overrightarrow{AM}=x\overrightarrow{AB}$，$\overrightarrow{AN}=y\overrightarrow{AC}$，则x+4y的最小值是（ ）| A． | $\frac{9}{4}$ | B． | 2 | C． | $\sqrt{3}$ | D． | 1 |
分析 根据题意，画出图形，结合图形，利用$\overrightarrow{MH}$与$\overrightarrow{NH}$共线，求出x与y的表达式，
再利用基本不等式求出x+4y的最小值即可．
解答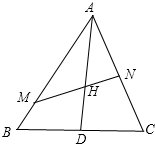 
解：如图所示，；
△ABC中，D为BC边的中点，H为AD的中点，
且$\overrightarrow{AM}$=x$\overrightarrow{AB}$，$\overrightarrow{AN}$=y$\overrightarrow{AC}$，
∴$\overrightarrow{AH}$=$\overrightarrow{AM}$+$\overrightarrow{MH}$=x$\overrightarrow{AB}$+$\overrightarrow{MH}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{4}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），
∴$\overrightarrow{MH}$=（$\frac{1}{4}$-x）$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$，
同理，$\overrightarrow{NH}$=$\frac{1}{4}$$\overrightarrow{AB}$+（$\frac{1}{4}$-y）$\overrightarrow{AC}$；
又$\overrightarrow{MH}$与$\overrightarrow{NH}$共线，
∴存在实数λ，使$\overrightarrow{MH}$=λ$\overrightarrow{NH}$（λ＜0），
即（$\frac{1}{4}$-x）$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$=λ[$\frac{1}{4}$$\overrightarrow{AB}$+（$\frac{1}{4}$-y）$\overrightarrow{AC}$]；
∴$\left\{\begin{array}{l}{\frac{1}{4}-x=\frac{1}{4}λ}\\{\frac{1}{4}=（\frac{1}{4}-y）λ}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=\frac{1}{4}（1-λ）}\\{y=\frac{1}{4}（1-\frac{1}{λ}）}\end{array}\right.$；
∴x+4y=$\frac{1}{4}$（1-λ）+（1-$\frac{1}{λ}$）
=-$\frac{1}{4}$λ+$\frac{1}{-λ}$+$\frac{5}{4}$≥2$\sqrt{（-\frac{1}{4}λ）•\frac{1}{-λ}}$+$\frac{5}{4}$=$\frac{9}{4}$，
当且仅当λ=-2时，“=”成立；
∴x+4y的最小值是$\frac{9}{4}$．
故选：A．
点评 本题考查了基本不等式的应用问题，也考查了平面向量的加法与减法运算问题，是中档题目．
