题目内容
6．函数$y=tan\frac{x}{a}$的最小正周期是（ ）| A． | aπ | B． | |a|π | C． | $\frac{π}{a}$ | D． | $\frac{π}{|a|}$ |
分析 直接利用正切函数的周期，求出函数的周期即可．
解答 解：函数$y=tan\frac{x}{a}$的最小正周期是T=$\frac{π}{|\frac{1}{a}|}$=|a|π．
故选：B．
点评 本题是基础题，考查三角函数的周期的求法，考查计算能力．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
10．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知cosB=-$\frac{1}{2}$．
（1）求sinAsinC的取值范围；
（2）若b=2$\sqrt{3}$，求△ABC面积的最大值．
（1）求sinAsinC的取值范围；
（2）若b=2$\sqrt{3}$，求△ABC面积的最大值．
17．已知直线l的参数方程为$\left\{\begin{array}{l}x=1+\frac{t}{2}\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数），则其直角坐标方程为（ ）
| A． | $\sqrt{3}$x+y+2-$\sqrt{3}$=0 | B． | $\sqrt{3}$x-y+2-$\sqrt{3}$=0 | C． | x-$\sqrt{3}$y+2-$\sqrt{3}$=0 | D． | x+$\sqrt{3}$y+2-$\sqrt{3}$=0 |
14．函数y=sin（$\frac{π}{3}$-2x）的单调减区间是（ ）
| A． | [2kπ-$\frac{π}{12}$，2kπ+$\frac{5π}{12}$]（k∈Z） | B． | [kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]（k∈Z） | ||
| C． | [2kπ+$\frac{5π}{12}$，2kπ+$\frac{11π}{12}$]（k∈Z） | D． | [kπ+$\frac{5π}{12}$，kπ+$\frac{11π}{12}$]（k∈Z） |
1．已知sinx=-$\frac{\sqrt{2}}{2}$、$\frac{π}{2}$＜x＜$\frac{3π}{2}$，则角x=（ ）
| A． | $\frac{4π}{3}$ | B． | $\frac{3π}{4}$ | C． | $\frac{5π}{4}$ | D． | $\frac{7π}{4}$ |
11．在△ABC中，$a=7，b=4\sqrt{3}，c=\sqrt{13}$，则△ABC的最小角为（ ）
| A． | 60° | B． | 30° | C． | 15° | D． | 45° |
18．如图所示描述错误的是（ ）
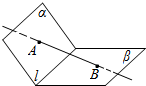
| A． | A∈α，B∈β | B． | α∩β=l | C． | AB∩α=A | D． | 直线AB与l相交 |