题目内容
10.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cosB=-$\frac{1}{2}$.(1)求sinAsinC的取值范围;
(2)若b=2$\sqrt{3}$,求△ABC面积的最大值.
分析 (1)由题意可得B=120°,A+C=60°.再利用积化和差公式化简sinAsinC 为$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$.再根据再根据-60°<A-C<60°,利用余弦函数的定义域和值域求得sinAsinC的取值范围.
(2)由条件利用余弦定理、基本不等式求得ac的最大值,从而求得△ABC面积的最大值的最大值.
解答 解:(1)△ABC中,由cosB=-$\frac{1}{2}$,可得B=120°,A+C=60°.
∴sinAsinC=$\frac{1}{2}$[cos(A-C)-cos(A+C)]=$\frac{1}{2}$[cos(A-C)-$\frac{1}{2}$]=$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$.
再根据-60°<A-C<60°,可得cos(A-C)∈($\frac{1}{2}$,1),$\frac{1}{2}$cos(A-C)∈($\frac{1}{4}$,$\frac{1}{2}$),
∴$\frac{1}{2}$cos(A-C)-$\frac{1}{4}$∈(0,$\frac{1}{4}$),即sinAsinC的取值范围为(0,$\frac{1}{4}$).
(2)若b=2$\sqrt{3}$,由余弦定理可得b2=12=a2+c2-2ac•cosB≥2ac+ac=3ac,
即ac≤4,当且仅当a=c=2时,取等号,故ac的最大值为4,
故△ABC面积为$\frac{1}{2}$ac•sin120°≤$\sqrt{3}$.
点评 本题主要考查积化和差公式、余弦定理、余弦函数的定义域和值域,基本不等式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知实数x,一满足$\left\{\begin{array}{l}{y≥\frac{x}{3}-2}\\{y≤2x+4}\\{2x+3y-12≤0}\end{array}\right.$,直线(2+λ)x-(3+λ)y+(1-2λ)=0(λ∈R)过定点A(x0,y0),则$\frac{y-{y}_{0}}{x-{x}_{0}}$的取值范围为( )
| A. | [$\frac{1}{5}$,7] | B. | [$\frac{1}{7}$,5] | C. | (-∞,$\frac{1}{5}$]∪[7,+∞] | D. | (-∞,$\frac{1}{7}$]∪[5,+∞] |
6.函数$y=tan\frac{x}{a}$的最小正周期是( )
| A. | aπ | B. | |a|π | C. | $\frac{π}{a}$ | D. | $\frac{π}{|a|}$ |
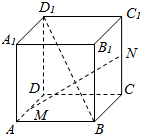 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.