题目内容
9.设f(x)=$\frac{{2}^{x}}{{2}^{x}+\sqrt{2}}$,试求:(1)f(a)+f(1-a)的值;
(2)f($\frac{1}{2010}$)+f($\frac{2}{2010}$)+…+f($\frac{2010}{2010}$)的值.
分析 (1)直接利用函数的解析式化简求解即可.
(2)由(1)得:f(x)+f(1-x)=1,进而可得f($\frac{1}{2010}$)+f($\frac{2}{2010}$)+…+f($\frac{2010}{2010}$)=f(x)+f(1-x).
解答 解:(1)f(x)=$\frac{{2}^{x}}{{2}^{x}+\sqrt{2}}$,f(a)+f(1-a)=$\frac{{2}^{a}}{{2}^{a}+\sqrt{2}}$+$\frac{{2}^{1-a}}{{2}^{1-a}+\sqrt{2}}$=$\frac{{2}^{a}}{{2}^{a}+\sqrt{2}}$+$\frac{{2}^{1-a}•{2}^{a}}{{2}^{1-a}•{2}^{a}+\sqrt{2}•{2}^{a}}$=$\frac{{2}^{a}}{{2}^{a}+\sqrt{2}}$+$\frac{\sqrt{2}}{{2}^{a}+\sqrt{2}}$=1
(2)由(1)得:f(a)+f(1-a)=1,
∴f($\frac{1}{2010}$)+f($\frac{2}{2010}$)+…+f($\frac{2010}{2010}$)=$\frac{1}{2}$×2010[f(a)+f(1-a)]+f(1)=1005+$\frac{{2}^{1}}{{2}^{1}+\sqrt{2}}$
=1005+2-$\sqrt{2}$
=1007-$\sqrt{2}$.
点评 本题考查的知识点是函数的对称性,其中熟练掌握函数对称变换法则,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.如图是关于闰年的程序框图,则以下年份是闰年的为( )
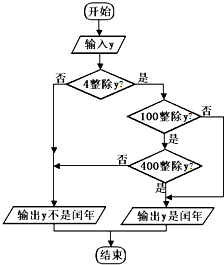

| A. | 2014年 | B. | 2010年 | C. | 2100年 | D. | 2012年 |
19.根据如图所示的程序框图(其中[x]表示不大于x的最大整数),输出r等于( )
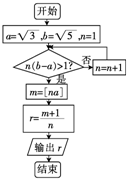

| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |