题目内容
点(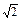 ,2)在幂函数f(x)的图象上,点(-2,
,2)在幂函数f(x)的图象上,点(-2,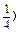 在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).
在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).
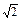 ,2)在幂函数f(x)的图象上,点(-2,
,2)在幂函数f(x)的图象上,点(-2,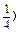 在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).
在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).①当x>1或x<-1时,
f(x)>g(x);
②当x=±1时,f(x)=g(x);
③当-1<x<1且x≠0时,
f(x)<g(x).
f(x)>g(x);
②当x=±1时,f(x)=g(x);
③当-1<x<1且x≠0时,
f(x)<g(x).
设f(x)=xα,则由题意得2=(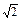 )α,
)α,
∴α=2,即f(x)=x2,再设g(x)=xβ,
则由题意得 =(-2)β,
=(-2)β,
∴β=-2,即g(x)=x-2,在同一坐标系中作出f(x)与g(x)的图象,如图所示.
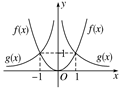 由图象可知:
由图象可知:
①当x>1或x<-1时,
f(x)>g(x);
②当x=±1时,f(x)=g(x);
③当-1<x<1且x≠0时,
f(x)<g(x).
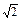 )α,
)α,∴α=2,即f(x)=x2,再设g(x)=xβ,
则由题意得
 =(-2)β,
=(-2)β,∴β=-2,即g(x)=x-2,在同一坐标系中作出f(x)与g(x)的图象,如图所示.
 由图象可知:
由图象可知:①当x>1或x<-1时,
f(x)>g(x);
②当x=±1时,f(x)=g(x);
③当-1<x<1且x≠0时,
f(x)<g(x).

练习册系列答案
相关题目
 (m为不等于0的偶数,n为奇数,且m·n<0),那么它的大致图象是( )
(m为不等于0的偶数,n为奇数,且m·n<0),那么它的大致图象是( )

 的单调区间,并比较f(-π)与f(-
的单调区间,并比较f(-π)与f(- 的大小.
的大小.
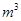 ,高为
,高为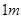 的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)
的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)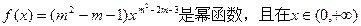 上是减函数,则实数m=( )
上是减函数,则实数m=( )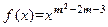 (m∈Z)为偶函数,且在区间(0,+∞)上是单调递减函数,则m= .
(m∈Z)为偶函数,且在区间(0,+∞)上是单调递减函数,则m= . 既是幂函数又是反比例函数,则这个函数是
既是幂函数又是反比例函数,则这个函数是