题目内容
已知幂函数y=f(x)的图象经过点(2,4),对于偶函数y=g(x)(x∈R),当x≥0时,g(x)=f(x)-2x.
(1)求函数y=f(x)的解析式;
(2)求当x<0时,函数y=g(x)的解析式,并在给定坐标系下,画出函数y=g(x)的图象;
(3)写出函数y=|g(x)|的单调递减区间.

(1)求函数y=f(x)的解析式;
(2)求当x<0时,函数y=g(x)的解析式,并在给定坐标系下,画出函数y=g(x)的图象;
(3)写出函数y=|g(x)|的单调递减区间.

(1)设y=f(x)=xα,代入点(2,4),得4=2α,
∴α=2,∴f(x)=x2;
(2)∵f(x)=x2 ,∴当x≥0时g(x)=x2-2x
设x<0,则-x>0,∵y=g(x)是R上的偶函数
∴g(x)=g(-x)=(-x)2-2(-x)=x2+2x
即当x<0时,g(x)=x2+2x,图象如右图所示;
(3)函数y=|g(x)|的图象如图
由图象知,函数y=|g(x)|的单调递减区间是:(-∞,-2],[-1,0],[1,2]

∴α=2,∴f(x)=x2;
(2)∵f(x)=x2 ,∴当x≥0时g(x)=x2-2x
设x<0,则-x>0,∵y=g(x)是R上的偶函数
∴g(x)=g(-x)=(-x)2-2(-x)=x2+2x
即当x<0时,g(x)=x2+2x,图象如右图所示;
(3)函数y=|g(x)|的图象如图

由图象知,函数y=|g(x)|的单调递减区间是:(-∞,-2],[-1,0],[1,2]


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 <
< ,求实数m的取值范围.
,求实数m的取值范围.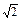 ,2)在幂函数f(x)的图象上,点(-2,
,2)在幂函数f(x)的图象上,点(-2,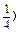 在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).
在幂函数g(x)的图象上,问当x为何值时,有f(x)>g(x),f(x)=g(x),f(x)<g(x).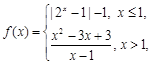 函数
函数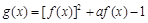 (其中a为常数),给出下列结论:
(其中a为常数),给出下列结论: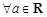 ,函数
,函数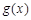 至少有一个零点;
至少有一个零点;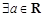 ,函数
,函数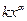 的图象过点
的图象过点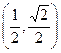 ,则
,则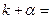 ___________
___________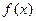 的图象经过点
的图象经过点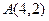 ,则它在A点处的切线方程
,则它在A点处的切线方程 为 ▲
为 ▲