题目内容
设抛物线y2=2px(p＞0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴,证明:直线AC经过原点O.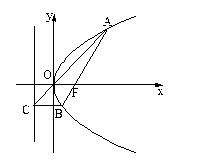
详见解析
解析试题分析：证明直线AC经过原点O，实质证明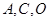
三点共线，即证直线
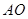与直线
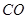的斜率相等. 设A(x1,y1)，则只需证
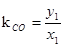即可.利用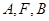
三点共线,可用A(x1,y1)表示出点B纵坐标为
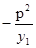，从而点C的坐标为(－
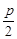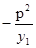,).因此直线CO的斜率为k=
=
=
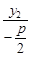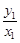,所以直线AC经过原点O.
试题解析：证:如图所示,因为抛物线y2=2px(p＞0)的焦点为F(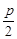,0)，所以经过点F的直线AB的方程可设为x=my+ 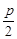2分
代入抛物线方程得y2－2pmy－p2=0.
若记A(x1,y1)、B(x2,y2)，则y1、y2是该方程的两个根，所以y1y2=－p2 7分.
因为BC∥x轴，且点C在准线x=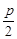－上，所以点C的坐标为(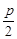－,y2).
故直线CO的斜率为k===,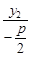
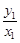即k也是直线OA的斜率，所以直线AC经过原点O. 12分
考点：直线与抛物线位置关系
练习册系列答案
相关题目
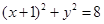上的动点，点
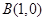.线段PB的垂直平分线与半径PA相交于点M，记点M的轨迹为Γ.
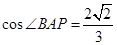时，求点M的坐标.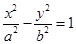
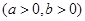的左焦点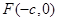
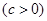，作倾斜角为
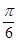的直线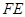
交该双曲线右支于点
，若
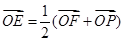，且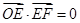
，则双曲线的离心率为__________．
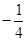，设顶点A的轨迹为曲线E．
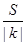的取值范围．
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,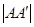
=4.
-
=1(a>0,b>0),离心率e=
,顶点到渐近线的距离为
.
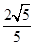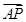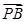=λ
,λ∈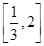
.求△AOB的面积的取值范围.
+
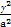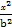=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=
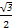,又椭圆经过点(
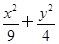＝1的焦点为F1、F2，点P为椭圆上的动点，当∠F1PF2为钝角时，求点P的横坐标x0的取值范围．