题目内容
如图,椭圆的中心为原点O,长轴在x轴上,离心率e= ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,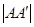 =4.
=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
(1) +
+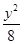 =1 (2)2
=1 (2)2 (x+
(x+ )2+y2=6,(x-
)2+y2=6,(x- )2+y2=6
)2+y2=6
解析解:(1)由题意知点A(-c,2)在椭圆上,则 +
+ =1,从而e2+
=1,从而e2+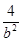 =1,
=1,
又e= ,故b2=
,故b2=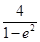 =8,从而a2
=8,从而a2 ==16.
==16.
故该椭圆的标准方程为 +
+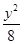 =1.
=1.
(2)由椭圆的对称性,可设Q(x0,0).又设M(x,y)是椭圆上任意一点,则|QM|2=(x-x0)2+y2=x2-2x0x+ +8×(1-
+8×(1- )=
)= (x-2x0)2-
(x-2x0)2- +8(x∈[-4,4]).
+8(x∈[-4,4]).
设P(x1,y1),由题意知,P是椭圆上到Q的距离最小的点,
因此,当x=x1时|QM|2取最小值,
又x1∈(-4,4),所以当x=2x0时|QM|2取最小值,
从而x1=2x0,且|QP|2=8- .
.
由对称性知P′(x1,-y1),故|PP′|=|2y1|,
所以S=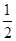 |2y1||x1-x0|
|2y1||x1-x0|
=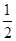 ×2
×2 |x0|
|x0|
=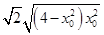
= ·
·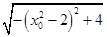 .
.
当x0=± 时,△PP′Q的面积S取得最大值2
时,△PP′Q的面积S取得最大值2 .
.
此时对应的圆Q的圆心坐标为Q(± ,0),半径|QP|=
,0),半径|QP|=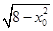 =
= ,
,
因此,这样的圆有两个,其标准方程分别为(x+ )2+y2=6,(x-
)2+y2=6,(x- )2+y2=6.
)2+y2=6.

练习册系列答案
相关题目
 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点 ,且
,且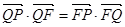 .
. 的方程;
的方程; 与曲线
与曲线 ,且与直线
,且与直线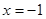 相交于点
相交于点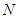 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点 ,使得以
,使得以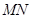 为直径的圆恒过此定点
为直径的圆恒过此定点 的右焦点为
的右焦点为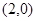 ,实轴长
,实轴长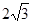 .
.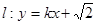 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点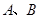 ,且
,且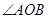 为锐角(其中
为锐角(其中 为原点),求
为原点),求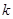 的取值范围.
的取值范围.
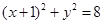 上的动点,点
上的动点,点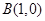 .线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.
.线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为Γ.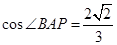 时,求点M的坐标.
时,求点M的坐标. +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: ,
, ),Q(
),Q(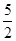 ,1),求椭圆C1的方程;
,1),求椭圆C1的方程;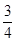 .
. 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当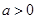 ,向量
,向量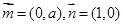 ,经过定点
,经过定点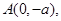 以
以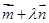 为方向向量的直线与经过定点
为方向向量的直线与经过定点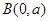 以
以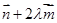 为方向向量的直线相交于
为方向向量的直线相交于 ,其中
,其中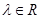 ,
,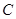 的方程;(2)若
的方程;(2)若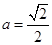 ,过
,过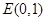 的直线交曲线
的直线交曲线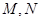 两点,求
两点,求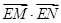 的取值范围。
的取值范围。