题目内容
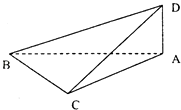
【题目】如图所示，在正方体ABCD﹣A1B1C1D1中，S是B1D1的中点，E，F，G分别是BC，CD和SC的中点．求证： 
（1）直线EG∥平面BDD1B1；
（2）平面EFG∥平面BDD1B1 ．
【答案】
（1）证明：如图，连结SB，
∵E，G分别是BC，SC的中点，
∴EG∥SB，
又SB平面BDD1B1，EG不包含于平面BDD1B1，
∴直线EG∥平面BDD1B1
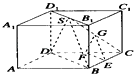
（2）证明：如图，连结SD，
∵F，G分别是DC，SC的中点，∴FG∥SD，
又SD平面BDD1B1，FG不包含于平面BDD1B1，
∴FG∥平面BDD1B1，
又直线EG∥平面BDD1B1，且直线EG平面EFG，直线FG平面EFG，
EG∩FG=G，
∴平面EFG∥平面BDD1B1
【解析】（1）连结SB，由已知得EG∥SB，由此能证明直线EG∥平面BDD1B1 ． （2）连结SD，由已知得FG∥SD，从而FG∥平面BDD1B1 ， 又直线EG∥平面BDD1B1 ， 由此能证明平面EFG∥平面BDD1B1 ．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对平面与平面平行的判定的理解，了解判断两平面平行的方法有三种:用定义；判定定理；垂直于同一条直线的两个平面平行．
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如下表所示：
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
（Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
（Ⅱ）欲使销售量为13杯，则价格应定为多少？
注：在回归直线y= 
中， 
， 
= 
﹣ 
． 
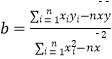=146.5．