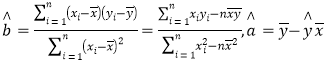Question

【题目】已知函数 ，（a为常数且a＞0）．
（1）若函数的定义域为 ，值域为 ，求a的值；
（2）在（1）的条件下，定义区间（m，n），[m，n]，（m，n]，[m，n）的长度为n﹣m，其中n＞m，若不等式f（x）+b＞0，x∈[0，π]的解集构成的各区间的长度和超过 ，求b的取值范围．

Answer 1

【答案】
（1）解：由三角函数公式化简可得：

f（x）=a（sinxcosx+ + cos2x）

=a（ sin2x+ + cos2x）

=a[ +sin（2x+ ）]，

∵x∈ ，∴2x+ ∈[ ， ]，

∴sin（2x+ ）∈[﹣ ，1]，

∴ +sin（2x+ ）∈[0，1+ ]，

∵由已知可得函数值域为 ，

∴a=1

（2）解：由题意可得 ，即

要使解集构成的各区间的长度和超过 ，需 ，解得

【解析】（1）由三角函数公式化简可得f（x）=a[ +sin（2x+ ）]，由已知函数的值域可得a值．（2）由题意可得 要使解集构成的各区间的长度和超过 ，需 ，解不等式可得．