题目内容
3.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|=$\frac{2\sqrt{3}}{3}$|$\overrightarrow{a}$|,则$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{6}$.分析 运用向量的平方即为模的平方,可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,再由向量的数量积的夹角公式计算即可得到所求值.
解答 解:由|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,两边平方可得,
($\overrightarrow{a}+\overrightarrow{b}$)2=($\overrightarrow{a}-\overrightarrow{b}$)2,即为$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2,
即有$\overrightarrow{a}$•$\overrightarrow{b}$=0,
则($\overrightarrow{a}+\overrightarrow{b}$)•$\overrightarrow{a}$=$\overrightarrow{a}$2+$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2,
即有cos<$\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{a}|}$=$\frac{|\overrightarrow{a}{|}^{2}}{\frac{2\sqrt{3}}{3}|\overrightarrow{a}{|}^{2}}$=$\frac{\sqrt{3}}{2}$,
由0≤<$\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{a}$>≤π,可得<$\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查向量的夹角的求法,注意运用向量的数量积的夹角公式和性质:向量的平方即为模的平方,考查运算能力,属于中档题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案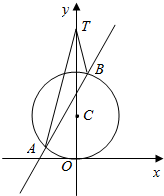 如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.
如图,已知圆C的圆心在y轴的正半轴上,且与x轴相切,圆C与直线y=kx+3相交于A,B两点.当$k=\sqrt{3}$时,$|AB|=\sqrt{15}$.