题目内容
【题目】设椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(I)结合离心率,得到a,b,c的关系,计算A的坐标,计算切线与椭圆交点坐标,代入椭圆方程,计算参数,即可。(II)分切线斜率存在与不存在讨论,设出M,N的坐标,设出切线方程,结合圆心到切线距离公式,得到m,k的关系式,将直线方程代入椭圆方程,利用根与系数关系,表示![]() ,结合三角形相似,证明结论,即可。
,结合三角形相似,证明结论,即可。
(Ⅰ)设椭圆的半焦距为![]() ,由椭圆的离心率为
,由椭圆的离心率为![]() 知,
知,![]() ,
,
∴椭圆![]() 的方程可设为
的方程可设为![]() .
.
易求得![]() ,∴点
,∴点![]() 在椭圆上,∴
在椭圆上,∴![]() ,
,
解得![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当过点![]() 且与圆
且与圆![]() 相切的切线斜率不存在时,不妨设切线方程为
相切的切线斜率不存在时,不妨设切线方程为![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() ,
,
![]() ,∴
,∴![]() .
.
当过点![]() 且与圆
且与圆![]() 相切的切线斜率存在时,可设切线的方程为
相切的切线斜率存在时,可设切线的方程为![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
联立直线和椭圆的方程得![]() ,
,
∴![]() ,得
,得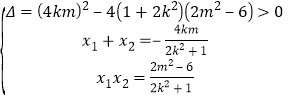 .
.
∵![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
∴![]() .
.
综上所述,圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,都有
,都有![]() .
.
在![]() 中,由
中,由![]() 与
与![]() 相似得,
相似得,![]() 为定值.
为定值.

【题目】某物流公司欲将一批海产品从A地运往B地,现有汽车、火车、飞机三种运输工具可供选择,这三种工具的主要参考数据如下:
运输工具 | 途中速度( | 途中费用(元/ | 装卸时间( | 装卸费用(元/ |
汽车 | 50 | 80 | 2 | 200 |
火车 | 100 | 40 | 3 | 400 |
飞机 | 200 | 200 | 3 | 800 |
若这批海产品在运输过程中的损耗为300元/![]() ,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
,问采用哪种运输方式比较好,即运输过程中的费用与损耗之和最小.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
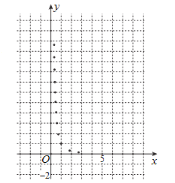
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关
关![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为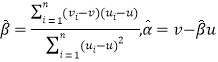 .
.
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 |
| 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;可供选择的数据:
;可供选择的数据:![]() ,
,![]() ;
;
(3)用![]() 表示用(2)中所求的线性回归方程得到的与
表示用(2)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的最小二乘估计分别为
的最小二乘估计分别为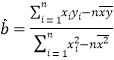 ,
,![]() )
)
