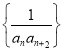Question

【题目】某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为 ，中奖可以获得2分；方案乙的中奖率为P0（0＜P0＜1），中奖可以获得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品． （Ⅰ）张三选择方案甲抽奖，李四选择方案乙抽奖，记他们的累计得分为X，若X≤3的概率为 ，求P0；
（Ⅱ）若张三、李四两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？

Answer 1

【答案】解：（Ⅰ）由已知得，张三中奖的概率为 ，李四中奖的概率为P0 ， 且两人中奖与否互不影响． 记“这2人的累计得分X≤3”的事件为A，则事件A的对立事件为“X=5”，
因为P（X=5）= ×P0 ， 所以P（A）=1﹣P（X=5）=1﹣ ×P0= ，
所以 ．
（Ⅱ）设张三、李四都选择方案甲抽奖中奖次数为X1 ， 都选择方案乙抽奖中奖次数为X2 ，
则这两人选择方案甲抽奖累计得分的数学期望为E（2X1），
选择方案乙抽奖累计得分的数学期望为E（3X2）．
由已知可得，X1～B（2， ），X2～B（2，P0），
所以E（X1）=2× = ，E（X2）=2×P0 ，
从而E（2X1）=2E（X1）= ，E（3X2）=3E（X2）=6P0 ．
若E（2X1）＞E（3X2），则 ＞6P0 ， 所以0＜P0＜ ；
若E（2X1）＜E（3X2），则 ＜6P0 ， 所以 ＜P0＜1；
若E（2X1）=E（3X2），则 =6P0 ， 所以P0=
【解析】（Ⅰ）记“这2人的累计得分X≤3”的事件为A，则事件A的对立事件是“X=5”，由题意知，先根据相互独立事件的乘法公式求出对立事件的概率，再利用对立事件的概率公式，结合X≤3的概率为 ，即可求P0；（Ⅱ）设张三、李四两人都选择甲方案抽奖中奖次数为X1 ， 张三、李四两人都选择方案乙抽奖中奖次数为X2 ， 则这两人都选择甲方案抽奖累计得分的数学期望为E（2X1），都选择乙方案抽奖累计得分的数学期望为E（3X2）．根据题意知X1～B（2， ），X2～B（2，P0），利用贝努利概率的期望公式计算，再分类讨论，从而得出答案．