题目内容
关于x的不等式
>0的解集是{x|-3<x<-1或x>2},则实数a的值为( )
| x+a |
| x2+4x+3 |
A、-
| ||
| B、-2 | ||
C、
| ||
| D、2 |
分析:不等式
>0的解集为{x|-3<x<-1或x>2},故2是方程x+a=0的根,由根与系数的关系求出a即得.
| x+a |
| x2+4x+3 |
解答:解:由题意不等式
>0的解集为{x|-3<x<-1或x>2},故2是方程x+a=0的根,,
∴-a=2,
a=-2.
故选B
| x+a |
| x2+4x+3 |
∴-a=2,
a=-2.
故选B
点评:本题考查一元二次不等式与一元二次方程的关系,解答本题的关键是根据不等式的解集得出不等式相应方程的根,再由根与系数的关系求参数的值.注意总结方程,函数,不等式三者之间的联系.

练习册系列答案
相关题目
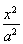




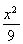




 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线 的焦点重合,则椭圆的方程为( )
的焦点重合,则椭圆的方程为( )


