题目内容
设函数f(x)＝ax2＋bx＋c，且f(1)＝－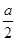
，3a＞2c＞2b，求证：
(1)a＞0，且－3＜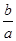
＜－
；
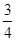(2)函数f(x)在区间(0,2)内至少有一个零点；
(3)设x1，x2是函数f(x)的两个零点，则
≤|x1－x2|＜
.
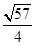（1）－3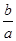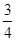＜＜－（2）函数f(x)在区间(0,2)内至少有一个零点．（3）见解析
解析
练习册系列答案
相关题目
题目内容
设函数f(x)＝ax2＋bx＋c，且f(1)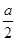＝－，3a＞2c＞2b，求证：
(1)a＞0，且－3＜＜－；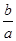
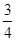(2)函数f(x)在区间(0,2)内至少有一个零点；
(3)设x1，x2是函数f(x)的两个零点，则≤|x1－x2|＜.
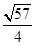（1）－3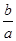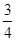＜＜－（2）函数f(x)在区间(0,2)内至少有一个零点．（3）见解析
解析
在区间[－1，1]上是增函数．
的两个相异实根，若对任意a∈A及t∈[－1，1]，不等式m2＋tm＋1≥|x1－x2|恒成立，求实数m的取值范围．
，其中
是仪器的月产量．
表示为月产量
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
.
)+f(-
)内各有一个零点,求实数a的范围.
吨收取的污水处理费
元，运行程序如下所示：请写出y与m的函数关系，并求排放污水150吨的污水处理费用.
－lg
＋lg12.5－log89·log278；