题目内容
4.正三角形的一个顶点恰好为抛物线y2=2px(p>0)的顶点,另两个顶点在抛物线上,则此三角形的边长为4$\sqrt{3}$p.分析 根据抛物线的对称性可知,若正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,则另外两个定点关于x轴对称,就可的直线OA的倾斜角,据此求出直线OA的方程,与抛物线方程联立解出A点坐标,就可求出正三角形的边长.
解答 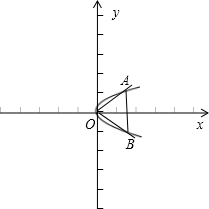 解:∵抛物线y2=2px关于x轴对称,
解:∵抛物线y2=2px关于x轴对称,
∴若正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,
则A,B点关于x轴对称,
∴直线OA倾斜角为30°,斜率为$\frac{\sqrt{3}}{3}$
∴直线OA方程为y=$\frac{\sqrt{3}}{3}$x,
代入抛物线方程,可得A(6p,2$\sqrt{3}$p),则B(6p,-2$\sqrt{3}$p),
∴|AB|=4$\sqrt{3}$p
∴这个正三角形的边长为4$\sqrt{3}$p
故答案为:4$\sqrt{3}$p.
点评 本题主要考查了抛物线的对称性,直线方程的点斜式,以及曲线交点的求法,属于圆锥曲线的综合题.

练习册系列答案
相关题目
14.已知点A(-2,-2),B(2,0),C(1,3),D(x,2),若$\overrightarrow{AB}$∥$\overrightarrow{CD}$,则x=( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | -1 |
9.已知f(sinx)=3-cos2x,则f(cosx)=( )
| A. | 3-cos2x | B. | 3-sin2x | C. | 3+cos2x | D. | 3+sin2x |
16.设X~B(10,0.8)则k=( )时,P(x=k)最大.
| A. | 8 | B. | 9 | C. | 8或9 | D. | 7或8 |
13. 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
14.4×5×6×…×(n-1)×n=( )
| A. | Cn4 | B. | n!-3! | C. | Ann-3 | D. | Cnn-3 |