题目内容
8．△ABC中，若a4+b4+c4=2c2（a2+b2），则角C的度数是45°或135°．分析 把已知等式a4+b4+c4=2c2（a2+b2），通过完全平方式、拆分项转化为（a2+b2-c2+$\sqrt{2}$ab）（a2+b2-c2-$\sqrt{2}$ab）=0．分两种情况，根据余弦定理即可求得C的度数．
解答 解：∵a4+b4+c4=2c2（a2+b2），
∴（a2+b2）2-2c2（a2+b2）+c4-2a2b2=0，
∴（a2+b2-c2）2-2a2b2=0，
∴（a2+b2-c2+$\sqrt{2}$ab）（a2+b2-c2-$\sqrt{2}$ab）=0
∴a2+b2-c2+$\sqrt{2}$ab=0或a2+b2-c2-$\sqrt{2}$ab=0
∵cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$，
∴cosC=-$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$，
∵0°＜C＜180°，
∴C=45°或135°．
故答案为：45°或135°．
点评 本题考查了余弦定理以及因式分解的应用，解决本题的关键是将原式转化为（a2+b2-c2+$\sqrt{2}$ab）（a2+b2-c2-$\sqrt{2}$ab）=0，属于中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
17．若圆M在x轴与y轴上截得的弦长总相等，则圆心M的轨迹方程是（ ）
| A． | x-y=0 | B． | x+y=0 | C． | x2+y2=0 | D． | x2-y2=0 |
7．
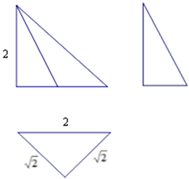一个几何体的三视图如图．该几何体的各个顶点都在球O的球面上，球O的体积为（ ）
一个几何体的三视图如图．该几何体的各个顶点都在球O的球面上，球O的体积为（ ）| A． | $\frac{\sqrt{2}}{3}$π | B． | $\frac{4\sqrt{2}}{3}$π | C． | $\frac{8\sqrt{2}}{3}$π | D． | $\frac{10\sqrt{2}}{3}$π |