题目内容
已知函数 ,
,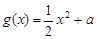 (
( 为常数),直线
为常数),直线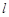 与函数
与函数 、
、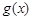 的图象都相切,且
的图象都相切,且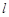 与函数
与函数 图象的切点的横坐标为
图象的切点的横坐标为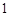 .
.
(1)求直线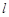 的方程及
的方程及 的值;
的值;
(2)若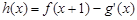 [注:
[注: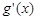 是
是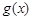 的导函数],求函数
的导函数],求函数 的单调递增区间;
的单调递增区间;
(3)当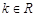 时,试讨论方程
时,试讨论方程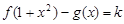 的解的个数.
的解的个数.
(1)  ;
;  ;(2)
;(2)  ,
,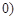 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)利用函数在 处的导数,等于在
处的导数,等于在 处切线的斜率,所以先求
处切线的斜率,所以先求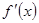 ,再求
,再求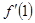 ,直线
,直线 的斜率就是
的斜率就是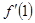 ,直线
,直线 过点
过点 ,代入得到直线
,代入得到直线 的方程,直线
的方程,直线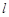 与
与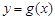 的图象相切,所以代入联立
的图象相切,所以代入联立 ,
, 得到
得到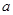 值;(2)先求
值;(2)先求 , 得到
, 得到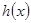 ,再求
,再求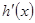 ,令
,令 ,得到
,得到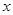 的取值范围,即求得函数
的取值范围,即求得函数 的单调递增区间;(3)令
的单调递增区间;(3)令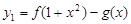
 ,
, ,再求
,再求 ,得到极值点,然后列表分析当
,得到极值点,然后列表分析当 变化时,
变化时, ,
, 的变化情况,结合
的变化情况,结合 为偶函数,画出
为偶函数,画出 的函数图形,再画
的函数图形,再画 ,当直线
,当直线 上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同
上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同 的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题.
的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题.
试题解析:(1)解:由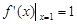 ,
,
故直线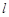 的斜率为
的斜率为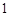 ,切点为
,切点为 ,
,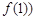 ,即
,即 ,
,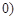 ,
,
所以直线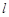 的方程为
的方程为 . 3分
. 3分
直线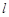 与
与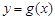 的图象相切,等价于方程组
的图象相切,等价于方程组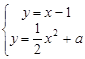 只有一解,
只有一解,
即方程 有两个相等实根,
有两个相等实根,
所以令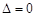 ,解得
,解得 . 5分
. 5分
(2)因为
 ,
,
由 ,
,
令 ,所以
,所以 ,
,
所以函数 的单调递增区间是
的单调递增区间是 ,
,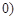 . 8分
. 8分
(3)令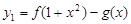
 ,
, ,
,
由 ,令
,令 ,得
,得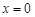 ,
, ,
,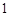 , 10分
, 10分
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
 ,
,

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
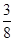 时,判断方程f(x)=-
时,判断方程f(x)=-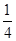 的实数根的个数,并说明理由.
的实数根的个数,并说明理由. x2+6x-a.
x2+6x-a.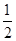 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R. 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.  的值;
的值;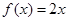 根的个数,并证明你的结论;
根的个数,并证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.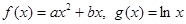 .
.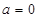 时,①若
时,①若 的图象与
的图象与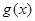 的图象相切于点
的图象相切于点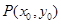 ,求
,求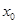 及
及 的值;
的值;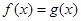 在
在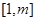 上有解,求
上有解,求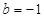 时,若
时,若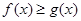 在
在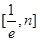 上恒成立,求
上恒成立,求 的取值范围.
的取值范围. 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于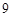 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
 取
取 )
) 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 元
元