题目内容
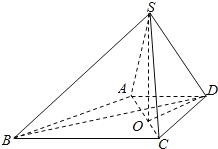
【题目】如图所示,在底面为梯形的四棱锥S﹣ABCD中,已知AD∥BC,∠ASC=60°,![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(1)求证:AC⊥SD;
(2)求三棱锥B﹣SAD的体积.

【答案】(1)见解析;(2)![]()
【解析】
(1)取AC中点O,连结OD,SO,由等腰三角形的性质可知AC⊥SO,AC⊥OD,故AC⊥平面SOD,于是AC⊥SD;
(2)由△ASC是等边三角形可求得SO,AC,结合已知条件,利用勾股定理得AD⊥CD,SO⊥OD,故SO⊥平面ABCD,再利用三棱锥体积转化计算即可.
(1)取AC中点O,连结OD,SO,∵SA=SC,∴SO⊥AC,∵AD=CD,∴OD⊥AC,
又∵OS平面SOD,OD平面SOD,OS∩OD=O,∴AC⊥平面SOD,∵SD平面SOD,∴AC⊥SD.
(2)∵SA=SC=2,∠ASC=60°,∴△ASC是等边三角形,∴AC=2,OS=![]() ,
,
∵AD=CD=![]() ,∴AD2+CD2=AC2,∴∠ADC=90°,OD=
,∴AD2+CD2=AC2,∴∠ADC=90°,OD=![]() =1.
=1.
∵SD=2,∴SO2+OD2=SD2,∴SO⊥OD,
又∵SO⊥AC,AC平面ABCD,OD平面ABCD,AC∩OD=O,∴SO⊥平面ABCD,
∴V棱锥B﹣SAD=V棱锥S﹣ABD=![]() S△ABDSO=
S△ABDSO=![]() .
.

【题目】工厂抽取了在一段时间内生产的一批产品,测量一项质量指标值,绘制了如图所示的频率分布直方图.
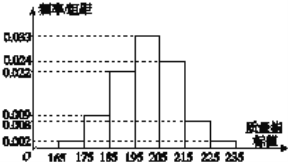
(1)计算该样本的平均值![]() ,方差
,方差![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
(2)若质量指标值在![]() 之内为一等品.
之内为一等品.
(i)用样本估计总体,问该工厂一天生产的产品是否有![]() 以上为一等品?
以上为一等品?
(ii)某天早上、下午分别抽检了50件产品,完成下面的表格,并根据已有数据,判断是否有![]() 的把握认为一等品率与生产时间有关?
的把握认为一等品率与生产时间有关?
一等品个数 | 非一等品个数 | 总计 | |
早上 | 36 | 50 | |
下午 | 26 | 50 | |
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
参考数据:![]() .
.