题目内容
在一次数学考试中,第22,23,24题为选做题,规定每位考生必须且只须在其中选做一题,设5名考生选做这三题的任意一题的可能性均为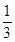 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
(1)求其中甲、乙两人选做同一题的概率;
(2)设选做第23题的人数为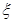 ,求
,求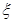 的分布列及数学期望.
的分布列及数学期望.
(1)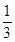 ;(2)
;(2)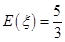 .
.
解析试题分析:(1) 设事件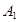 表示甲选22题,
表示甲选22题,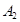 表示甲选23题,
表示甲选23题,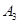 表示甲选24题,
表示甲选24题,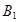 表示乙选22题,
表示乙选22题,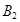 表示乙选23题,
表示乙选23题,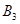 表示乙选24题,则甲、乙两人选做同一题事件为
表示乙选24题,则甲、乙两人选做同一题事件为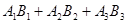 ,且
,且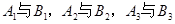 相互独立,根据相互独立事件概率的求法计算可得;(2)
相互独立,根据相互独立事件概率的求法计算可得;(2)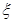 服从二项分布,根据二项分布概率的计算方法可列出分布列.
服从二项分布,根据二项分布概率的计算方法可列出分布列.
试题解析:(1)设事件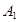 表示甲选22题,
表示甲选22题,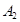 表示甲选23题,
表示甲选23题,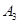 表示甲选24题,
表示甲选24题,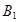 表示乙选22题,
表示乙选22题,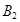 表示乙选23题,
表示乙选23题,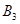 表示乙选24题,
表示乙选24题,
则甲、乙两人选做同一题事件为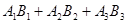 ,且
,且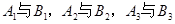 相互独立,
相互独立,
所以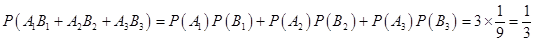 4分
4分
(2)设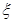 可能取值为0,1,2,3,4,5.
可能取值为0,1,2,3,4,5.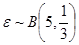
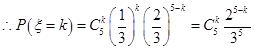 ,
,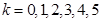
 分布列为
分布列为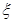
0 1 2 3 4 5 
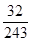
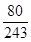
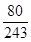
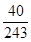
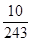
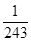
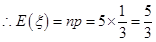 12分
12分
考点:1.相互独立事件概率的计算;2.二项分布的分布列和数学期望.

练习册系列答案
相关题目
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是
 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为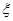 ,求
,求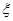 的分布列和数学期望.
的分布列和数学期望. 已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)根据上表,利用最小二乘法,求出
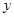 关于
关于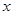 的线性回归方程
的线性回归方程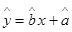 ,
,其中
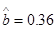
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.(四舍五入到整数)
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 |
| 温差(℃) | 9 | 10 | 8 | 11 |
| 发芽数(粒) | 33 | 39 | 26 | 46 |
(2)若研究的一个项目在这四天中任选2天的种子发芽数来进行,记发芽的种子数分别为m,n(m<n),则以(m,n)的形式列出所有的基本事件,并求“m,n满足
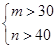 ”的事件A的概率.
”的事件A的概率.  表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求
 ,求随机变量
,求随机变量 .
.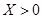 就去打球;若
就去打球;若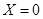 就去唱歌;若
就去唱歌;若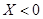 就去下棋.
就去下棋.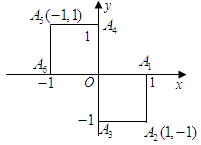
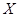 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求