题目内容
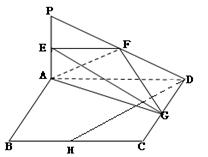
如图所示,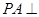 平面
平面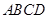 ,四边形
,四边形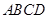 为正方形,且
为正方形,且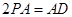 ,
,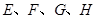 分别是线段
分别是线段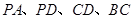 的中点.
的中点.
(Ⅰ)求证: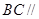 平面
平面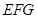 ;
;
(Ⅱ)求证: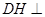 平面
平面 ;
;
(Ⅲ)求三棱锥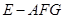 与四棱锥
与四棱锥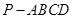 的体积比.
的体积比.
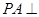 平面
平面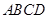 ,四边形
,四边形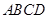 为正方形,且
为正方形,且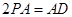 ,
,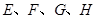 分别是线段
分别是线段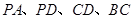 的中点.
的中点.
(Ⅰ)求证:
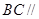 平面
平面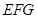 ;
;(Ⅱ)求证:
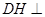 平面
平面 ;
;(Ⅲ)求三棱锥
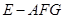 与四棱锥
与四棱锥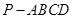 的体积比.
的体积比.(Ⅰ)见解析; (Ⅱ)见解析;(Ⅲ)三棱锥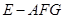 与四棱锥
与四棱锥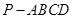 的体积比
的体积比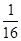
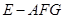 与四棱锥
与四棱锥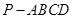 的体积比
的体积比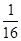
试题分析:(Ⅰ)通过证明
 ,
, ,从而有
,从而有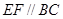 ,然后由直线和平面平行的判定定理可得
,然后由直线和平面平行的判定定理可得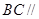 平面
平面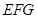 ;(Ⅱ)利用直线和平面垂直的性质定理可得AE⊥DH,再证DH⊥AG,由直线和平面垂直的判定定理可得
;(Ⅱ)利用直线和平面垂直的性质定理可得AE⊥DH,再证DH⊥AG,由直线和平面垂直的判定定理可得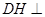 平面
平面 ;(Ⅲ)由已知可得
;(Ⅲ)由已知可得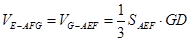 ,
,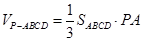 ,所以
,所以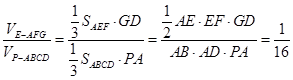 ,此问注意直线和平面关系的运用和体积的转化.
,此问注意直线和平面关系的运用和体积的转化.试题解析:(Ⅰ)
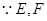 分别为
分别为 中点,所以AD∥EF,∵BC∥AD, ,∴BC∥EF....2分
中点,所以AD∥EF,∵BC∥AD, ,∴BC∥EF....2分
 ∥平面EFG............4分
∥平面EFG............4分(Ⅱ)∵PA⊥平面ABCD,∴PA⊥DH ,即 AE⊥DH..........
∵△ADG≌△DCH ,∴∠HDC=∠DAG,∠AGD+∠DAG=90°
∴∠AGD+∠HDC=90°
∴DH⊥AG
又∵AE∩AG=A,∴DH⊥平面AEG............8分
(Ⅲ)由PA⊥平面ABCD,得
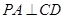 ,又
,又 ,所以
,所以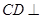 平面
平面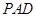 ,
,所以
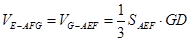 ,
,又
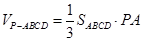
所以
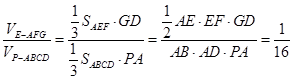 .........12分
.........12分
练习册系列答案
相关题目
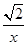 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.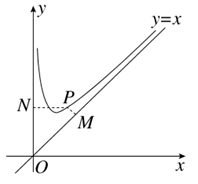
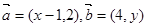 相互垂直,则点(2,3)到点(x,y)的距离的最小值为 .
相互垂直,则点(2,3)到点(x,y)的距离的最小值为 . 上的动点
上的动点 到直线
到直线 距离的最小值是 .
距离的最小值是 .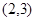 ,在
,在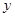 轴及直线
轴及直线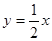 上各取一点
上各取一点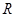 、
、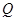 ,为使
,为使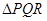 的周长最小,则
的周长最小,则 的切线,则此切线段的长度为_______.
的切线,则此切线段的长度为_______. 到直线
到直线 :
: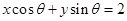 的距离的最大值为( )
的距离的最大值为( )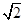


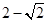
 求
求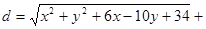
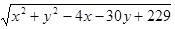 的最小值.
的最小值.