题目内容
6.已知关于x的不等式ax2+bx+4>0的解集是(-1,2),则不等式ax+b+4>0的解集是(-∞,3).分析 根据不等式与对应方程之间的关系,利用根与系数的关系求出a、b的值,再求不等式ax+b+4>0的解集.
解答 解:∵关于x的不等式ax2+bx+4>0的解集是(-1,2),
∴方程ax2+bx+4=0的实数根为-1和2,
由根与系数的关系,得$\left\{\begin{array}{l}{\frac{4}{a}=-1×2}\\{-\frac{b}{a}=-1+2}\end{array}\right.$,
解得a=-2,b=2;
∴不等式ax+b+4>0化为
-2x+2+4>0,
解得x<3,
∴该不等式的解集是(-∞,3).
故答案为:(-∞,3).
点评 本题考查了不等式的解法与应用问题,也考查了根与系数关系的应用问题,是基础题目.

练习册系列答案
相关题目
14.已知a>0,b>0,a+$\frac{1}{a}$+$\frac{b}{2}$+$\frac{8}{b}$=6,若直线y=mx+ab与不等式组$\left\{\begin{array}{l}x+y-3≥0\\ 2x-y≥0\\ x-2≤0\end{array}\right.$,表示的平面区域有公共点,则实数m的取值范围是( )
| A. | $[{-6,-\frac{3}{2}}]$ | B. | [-2,0] | C. | $[{-2,-\frac{3}{2}}]$ | D. | (-∞,-2] |
11.4名同学争夺三项冠军,冠军获得者的可能种数是( )
| A. | 43 | B. | $A_4^3$ | C. | $C_4^3$ | D. | 4 |
15.已知△ABC中,AB=2,$AC=\sqrt{2}BC$,则△ABC的面积的最大值为 ( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | $\frac{2}{3}$$\sqrt{3}$ |
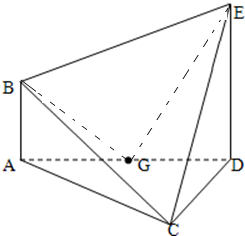 在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.
在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.