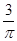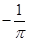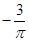题目内容
已知函数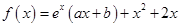 ,曲线
,曲线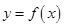 经过点
经过点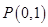 ,
,
且在点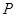 处的切线为
处的切线为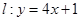 .
.
(1)求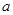 、
、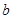 的值;
的值;
(2)若存在实数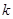 ,使得
,使得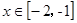 时,
时,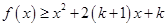 恒成立,求
恒成立,求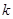 的取值范围.
的取值范围.
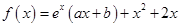 ,曲线
,曲线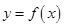 经过点
经过点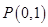 ,
,且在点
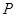 处的切线为
处的切线为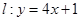 .
.(1)求
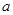 、
、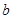 的值;
的值;(2)若存在实数
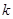 ,使得
,使得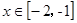 时,
时,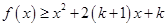 恒成立,求
恒成立,求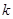 的取值范围.
的取值范围.(1)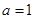 ,
,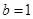 ;(2)
;(2)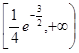 .
.
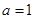 ,
,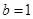 ;(2)
;(2)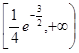 .
.试题分析:(1)利用条件“曲线
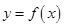 经过点
经过点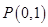 ,且在点
,且在点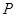 处的切线为
处的切线为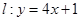 ”得到
”得到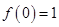 以及
以及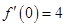 ,从而列出方程组求解
,从而列出方程组求解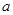 、
、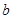 的值;(2)利用参数分离法将问题等价转化为
的值;(2)利用参数分离法将问题等价转化为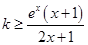 在区间
在区间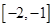 上恒成立,并构造新函数
上恒成立,并构造新函数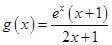 ,转化为
,转化为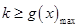 ,
,利用导数求出函数
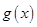 在区间
在区间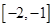 的最大值,从而可以求出实数
的最大值,从而可以求出实数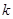 的取值范围.
的取值范围.(1)
 ,
,依题意,
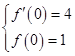 ,即
,即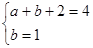 ,解得
,解得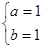 ;
;(2)由
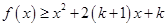 ,得:
,得: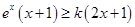 ,
,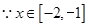 时,
时,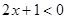
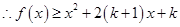 即
即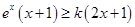 恒成立,当且仅当
恒成立,当且仅当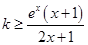 ,
, 设
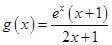 ,
,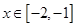 ,
,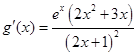 ,
,由
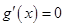 得
得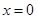 (舍去),
(舍去),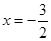 ,
,当
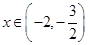 ,
,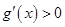 ;当
;当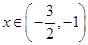 ,
,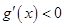 ,
,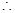
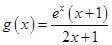 在区间
在区间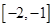 上的最大值为
上的最大值为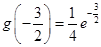 ,
, 所以常数
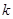 的取值范围为
的取值范围为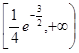 .
.
练习册系列答案
相关题目
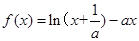 ,其中
,其中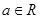 且
且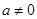 .
.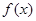 的单调性;
的单调性;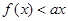 恒成立,求实数
恒成立,求实数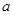 取值范围;
取值范围;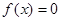 存在两个异号实根
存在两个异号实根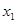 ,
,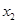 ,求证:
,求证: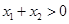
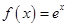 .
.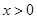 时,设
时,设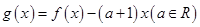 .讨论函数
.讨论函数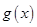 的单调性;
的单调性;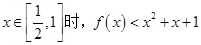 .
. 在点(1,0)处的切线.
在点(1,0)处的切线. 的导数
的导数 处取到极大值,则
处取到极大值,则 的取值范围是 .
的取值范围是 .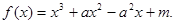
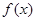 在
在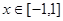 内没有极值点,求
内没有极值点,求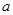 的取值范围;
的取值范围;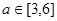 ,不等式
,不等式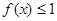 在
在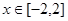 上恒成立,求实数
上恒成立,求实数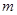 的取值范围.
的取值范围.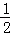 x2﹣lnx的单调递减区间为( )
x2﹣lnx的单调递减区间为( ) 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是 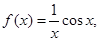 则
则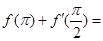 ( )
( )