题目内容
设集合A={x|x2+(p-3)x+q=0}={2},则p+q= .
考点:集合的表示法
专题:集合
分析:根据已知条件知道:2是方程x2+(p-3)x+q=0的二重根,所以由韦达定理可求出p,q,从而求出p+q.
解答:解:集合A={x|x2+(p-3)x+q=0}={2};
∴2是方程x2+(p-3)x+q=0的实数根,并且是二重根;
∴根据韦达定理得:
,解得p=-1,q=4;
∴p+q=3.
故答案为:3.
∴2是方程x2+(p-3)x+q=0的实数根,并且是二重根;
∴根据韦达定理得:
|
∴p+q=3.
故答案为:3.
点评:考查一元二次方程的实数根,当一元二次方程只有一个实数根时,这个实数根是二重根,以及对韦达定理的运用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知集合A={0,1,2,3},B={(x,y)|x∈A,y∈A,|x-y|∈A},则B中所含元素的个数为( )
| A、14 | B、16 | C、28 | D、32 |
设a、b∈R,且{a,
,1}={a2,a+b,0},则a2014+b2014等于( )
| b |
| a |
| A、0 | B、1 | C、2 | D、2014 |
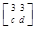 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1=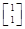 ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2= .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵.