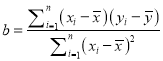题目内容
【题目】设
为不同的两点，直线
，下列命题正确的有（ ）．
①不论
为何值，点
都不在直线
上；
②若
，则过点
的直线与直线平行；
③若
，则直线经过
的中点；
④若
，则点在直线的同侧且直线与线段的延长线相交．
A.1个B.2个C.3个D.4个
【答案】D
【解析】
由
可得①正确，分
和
两种情况讨论可得直线
与直线
平行，可得②正确，当
时，可得到
，从而得到③正确，当
时可得
和
，然后可得④正确.
因为
中，，所以点
不在直线上，故①正确
当时，根据
得到
，化简得
，
即直线的斜率为
，又直线的斜率为，由①可知点不在直线上，
得到直线与直线平行
当时，可得直线与直线的斜率都不存在，也满足平行，故②正确
当时，得到
，化简得
而线段的中点坐标为
，所以直线经过的中点，故③正确
当时，得到
，所以
，
即，所以点
在直线的同侧
且，可得点
与点到直线的距离不等，
所以延长线与直线相交，故④正确
综上：命题正确的有4个
故选：D
练习册系列答案
相关题目
【题目】某大学餐饮中心为了了解新生的饮食习惯，在某学院大一年级100名学生中进行了抽样调查，发现喜欢甜品的占70%．这100名学生中南方学生共80人．南方学生中有20人不喜欢甜品．
（1）完成下列
列联表：
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
（2）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（3）已知在被调查的南方学生中有6名数学系的学生，其中2名不喜欢甜品；有5名物理系的学生，其中1名不喜欢甜品．现从这两个系的学生中，各随机抽取2人，记抽出的4人中不喜欢甜品的人数为X，求X的分布列和数学期望．
附：
．
