题目内容
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.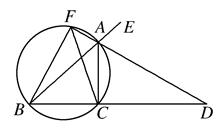
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.

见解析.
(1)证明本题的关键是∠FBC=∠FCB,需证:∠EAD=∠FAB=∠FCB,
需证:∠DAC=∠FBC.
(2)证明本题的关键是证:△FBA∽△FDB.
(3)解本题的关键是求得∠DAC= ∠EAC=60°,∠BAC=60°,∠D=30°.到此问题基本得以解决.
∠EAC=60°,∠BAC=60°,∠D=30°.到此问题基本得以解决.
(1)证明:∵AD平分∠EAC.
∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,∴∠FBC=∠FCB,
∴FB=FC.
(2)证明:∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD,
∴△FBA∽△FDB,∴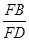 =
=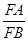 ,
,
∴FB2=FA·FD.
(3)∵AB是圆的直径,∴∠ACB=90°.
∵∠EAC=120°,∴∠DAC= ∠EAC=60°,∠BAC=60°.
∠EAC=60°,∠BAC=60°.
∴∠D=30°.∵BC=6 cm,∴AC=2 cm,∴AD=2AC=4
cm,∴AD=2AC=4 cm
cm
需证:∠DAC=∠FBC.
(2)证明本题的关键是证:△FBA∽△FDB.
(3)解本题的关键是求得∠DAC=
 ∠EAC=60°,∠BAC=60°,∠D=30°.到此问题基本得以解决.
∠EAC=60°,∠BAC=60°,∠D=30°.到此问题基本得以解决.(1)证明:∵AD平分∠EAC.
∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,∴∠FBC=∠FCB,
∴FB=FC.
(2)证明:∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD,
∴△FBA∽△FDB,∴
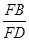 =
=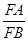 ,
,∴FB2=FA·FD.
(3)∵AB是圆的直径,∴∠ACB=90°.
∵∠EAC=120°,∴∠DAC=
 ∠EAC=60°,∠BAC=60°.
∠EAC=60°,∠BAC=60°.∴∠D=30°.∵BC=6 cm,∴AC=2
 cm,∴AD=2AC=4
cm,∴AD=2AC=4 cm
cm
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
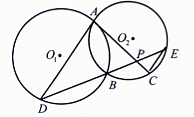
 ,一条直径的两个端点分别在
,一条直径的两个端点分别在 轴和
轴和 轴上,则此圆的方
轴上,则此圆的方


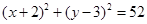
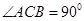 ,
,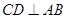 于点D,以BD为直径的圆与BC交于点E.则( )
于点D,以BD为直径的圆与BC交于点E.则( )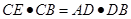



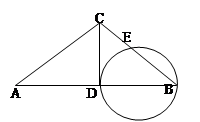
 0相切的圆的方程为 ( )
0相切的圆的方程为 ( )


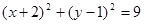
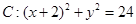 ,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足
,定点A(2,0),M为圆C上一动点,点P在AM上,点N在C、M上(C为圆心),且满足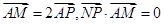 ,设点N的轨迹为曲线E.
,设点N的轨迹为曲线E.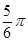 的直线
的直线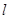 交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围.
交曲线E于C、D两点.若点Q(1,0)恰在以线段CD为直径的圆的内部,求实数m的取值范围. m),则sin2α=
m),则sin2α=
