题目内容
设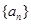 是公比大于1的等比数列,
是公比大于1的等比数列, 为其前
为其前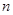 项和已知
项和已知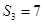 ,且
,且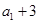 ,
,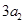 ,
,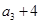 构成等差数列.
构成等差数列.
(Ⅰ)求数列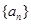 的通项公式;
的通项公式;
(Ⅱ)令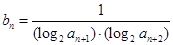 ,求数列
,求数列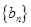 的前
的前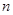 项和
项和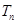 .
.
(I) ;(II)
;(II)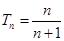 .
.
解析试题分析:(I)由题设“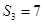 ,且
,且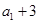 ,
,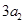 ,
,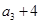 构成等差数列”得两个等式,由这两个等式便可求得公比和首项,从而得数列
构成等差数列”得两个等式,由这两个等式便可求得公比和首项,从而得数列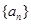 的通项公式.
的通项公式.
(II)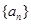 是公比大于1的等比数列,取对数便得等差数列,等差数列相邻两项的积的倒数构成的数列的和,就用裂项法.
是公比大于1的等比数列,取对数便得等差数列,等差数列相邻两项的积的倒数构成的数列的和,就用裂项法.
试题解析:(I) ,
, ,则
,则 ,
, .
.
则 ,故
,故 或
或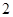 ,又
,又 ,则
,则 ,从而
,从而 .
.
(II)

 .
.
考点:1、等差数列与等比数列;2、数列的前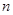 项和.
项和.

练习册系列答案
相关题目
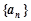 的前
的前 项和
项和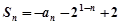 ,
, .
. 是等差数列;
是等差数列; ,求数列
,求数列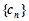 的前
的前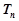 .
.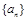 的前n项和为
的前n项和为 ,且
,且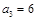 ,
,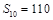 .设数列
.设数列 前n项和为
前n项和为 ,且
,且 ,求数列
,求数列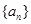 为等差数列,数列
为等差数列,数列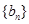 为等比数列且公比大于1,若
为等比数列且公比大于1,若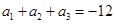 ,
,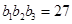 ,且
,且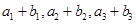 恰好是一各项均为正整数的等比数列的前三项.
恰好是一各项均为正整数的等比数列的前三项.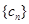 满足
满足
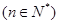 ,求
,求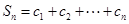 .
.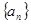 的前
的前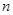 项的和为
项的和为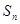 ,点
,点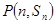
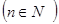 在函数
在函数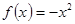
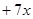 的图象上.
的图象上.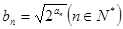 ,求数列
,求数列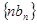 的前
的前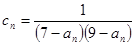 ,数列
,数列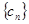 的前
的前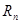 ,求使不等式
,求使不等式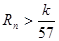 对一切
对一切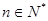 都成立的最大正整数
都成立的最大正整数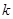 的值.
的值. 的前
的前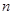 项和为
项和为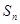 ,已知
,已知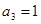 ,
,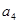 是
是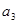 和
和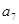 的等比中项.
的等比中项.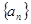 满足
满足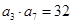 ,
,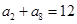 ,且
,且 (
(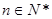 ).
).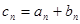 ,求数列
,求数列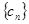 的前n项和
的前n项和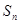 .
.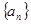 中,
中,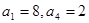 且满足
且满足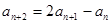 (
( 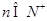 )
)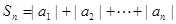 ,求
,求 ;
;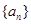 是公比大于
是公比大于 的等比数列,
的等比数列,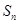 是
是 项和.若
项和.若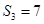 ,且
,且 ,
,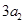 ,
, 构成等差数列.
构成等差数列.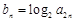 ,求数列
,求数列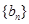 的前
的前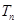 .
.