题目内容
已知数列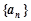 的前
的前 项和
项和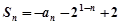 ,
, .
.
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)若 ,求数列
,求数列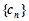 的前
的前 项和
项和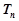 .
.
(I) 详见解析;(II)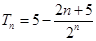 .
.
解析试题分析:(I) 求证:数列 是等差数列,首先确定数列
是等差数列,首先确定数列 的通项公式或关系式,由
的通项公式或关系式,由 ,求数列
,求数列 的通项公式或关系式,可利用
的通项公式或关系式,可利用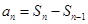 来求,注意需讨论
来求,注意需讨论 时的情况,本题由
时的情况,本题由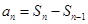 ,得到数列
,得到数列 的递推式,
的递推式, ,根据
,根据 ,证明
,证明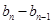 等于与
等于与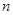 无关的常数即可;(Ⅱ)求数列
无关的常数即可;(Ⅱ)求数列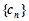 的前
的前 项和
项和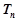 ,需求出数列
,需求出数列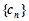 的通项公式,
的通项公式,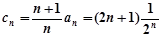 ,这是一个等比数列与一个等差数列对应项积所组成的数列,故可用错位相减法来求.
,这是一个等比数列与一个等差数列对应项积所组成的数列,故可用错位相减法来求.
试题解析:(I) ,当
,当 时,
时,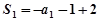 ,
,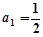 , 1分
, 1分
当 时,
时, , 2分
, 2分 ,
, 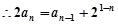 , 4分
, 4分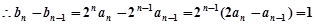 ,又
,又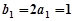 ,
, 是首项为1,公差为1的等差数列. 7分
是首项为1,公差为1的等差数列. 7分
(II) ,
, , 8分
, 8分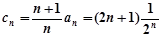 . 9分
. 9分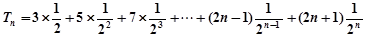 ,①
,① , ② 11分
, ② 11分
①-②得 ,
,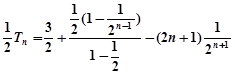
 , 13分
, 13分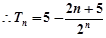 . 14分
. 14分
考点:求数列的通项公式,等差数列的定义,数列求和.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
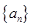 是公比为正数的等比数列,
是公比为正数的等比数列,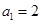 ,
, .
.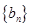 是首项为
是首项为 ,公差为
,公差为 的等差数列,求数列
的等差数列,求数列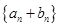 的前
的前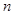 项和
项和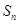 .
.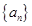 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数. ,
, ,
, ,求数列
,求数列 ,
, ,
, ,且
,且 ,求数列
,求数列 的等比数列.
的等比数列.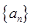 满足:
满足: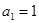 ,
,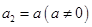 ,
,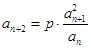 (其中
(其中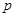 为非零常数,
为非零常数,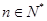 ).
).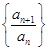 是不是等比数列?
是不是等比数列?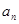 ;
;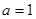 时,令
时,令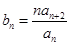 ,
,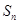 为数列
为数列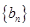 的前
的前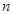 项和,求
项和,求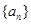 的首项
的首项 ,且满足
,且满足
 ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,求数列
,求数列 的前n项和
的前n项和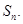
 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列, .
. .
.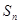 为其前n项和
为其前n项和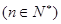 ,且
,且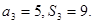
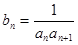 ,求数列
,求数列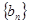 的前
的前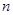 项和
项和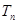 .
.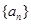 是公比大于1的等比数列,
是公比大于1的等比数列, 为其前
为其前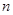 项和已知
项和已知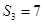 ,且
,且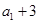 ,
,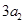 ,
,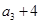 构成等差数列.
构成等差数列.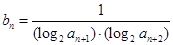 ,求数列
,求数列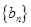 的前
的前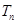 .
.