题目内容
2．
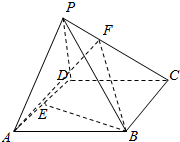如图所示，P为?ABCD所在平面外一点，E为AD的中点，F为PC上一点，当PA∥平面EBF时，$\frac{PF}{FC}$=$\frac{1}{2}$．
分析 连接AC交BE于点M，运用线面平行的性质定理，可得PA∥EM，再由平行线分线段成比例定理，可得结论．
解答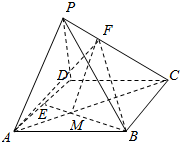 
解：连接AC交BE于点M，
连接FM．
∵PA∥平面EBF，PA?平面PAC，平面PAC∩平面EBF=EM，
∴PA∥EM，
∴$\frac{PF}{FC}$=$\frac{AM}{MC}$=$\frac{AE}{BC}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查的知识点是线面平行的性质定理，行线分线段成比例定理，难度中档．
练习册系列答案
小学教材完全解读系列答案
相关题目
12．已知函数f（x）是定义在R上的奇函数，当x＞0时，$f（x）=\frac{1}{2}（|{x-{a^2}}|-3{a^2}）$，若?x∈R，f（x-1）≤f（x），则实数a的取值范围为（ ）
| A． | $[-\frac{{\sqrt{2}}}{4}，\frac{{\sqrt{2}}}{4}]$ | B． | $[-\frac{1}{4}，\frac{1}{4}]$ | C． | $[-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}]$ | D． | $[-\frac{1}{2}，\frac{1}{2}]$ |
17．函数f（x）=b（1-$\frac{2}{1+{2}^{x}}$）+$\frac{a•（{4}^{x}-1）}{{2}^{x}}$+3（a、b为常数），若f（x）在（0，+∞）上有最大值11，则f（x）在（-∞，0）上有（ ）
| A． | 最大值10 | B． | 最小值-5 | C． | 最小值-4 | D． | 最大值5 |
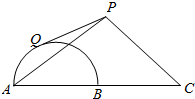在如图所示的平面中，点C为半圆的直径AB延长线上的一点，AB=BC=2，过动点P作半圆的切线PQ，若PC=$\sqrt{2}$PQ，则△PAC的面积的最大值为4$\sqrt{5}$．
14．设a=lg35，b=lg34，c=lg22，则（ ）
| A． | a＞b＞c | B． | c＞a＞b | C． | b＞a＞c | D． | b＞c＞a |