Question

8．已知函数f（x）=sin（2x-$\frac{π}{3}$）+$\frac{1}{2}$，x∈R
（Ⅰ）求函数y=f（x）的最大值及它的单调递增区间
（Ⅱ）将函数y=f（x）的图象向下平移$\frac{1}{2}$个单位，再向左平移$\frac{π}{3}$个单位得到函数y=g（x）的图象，若函数y=g（x）在x∈[0，$\frac{5π}{6}$]上的图象与直线y=m恰有两个不同的交点，求m的取值范围．

Answer 1

分析 （Ⅰ）根据函数的解析式利用正弦函数的最大值和单调性求得函数y=f（x）的最大值及它的单调递增区间
（Ⅱ）由条件利用函数y=Asin（ωx+φ）的图象变换规律，求得g（x）的解析式．令t=2x+$\frac{π}{3}$，则函数y=sint的图象和直线y=m在[$\frac{π}{3}$，2π]上有2个交点，数形结合求得m的范围．

解答 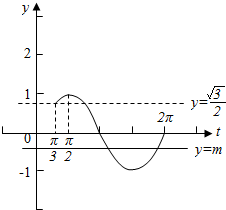解：（Ⅰ）对于函数f（x）=sin（2x-$\frac{π}{3}$）+$\frac{1}{2}$，它的最大值为1+$\frac{1}{2}$=$\frac{3}{2}$．
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$，k∈Z，求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$，可得函数的增区间为[kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，k∈Z．
（Ⅱ）将函数y=f（x）的图象向下平移$\frac{1}{2}$个单位，可得y=sin（2x-$\frac{π}{3}$）的图象，
再向左平移$\frac{π}{3}$个单位得到函数y=g（x）=sin[2（x+$\frac{π}{3}$）-$\frac{π}{3}$]=sin（2x+$\frac{π}{3}$）的图象．
由x∈[0，$\frac{5π}{6}$]，可得2x+$\frac{π}{3}$∈[$\frac{π}{3}$，2π]，令t=2x+$\frac{π}{3}$，则函数y=sint的图象和直线y=m在[$\frac{π}{3}$，2π]上有2个交点，
数形结合可得 $\frac{\sqrt{3}}{2}$≤m＜1 或-1＜m≤0．

点评 本题主要考查正弦函数的最大值和单调性，函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象特征，体现了转化、数形结合的数学思想，属于中档题．