题目内容
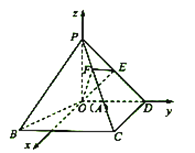
【题目】如图,已知抛物线![]() 和⊙
和⊙![]() :
:![]() ,过抛物线C上一点
,过抛物线C上一点![]() (
(![]() )做两条直线与⊙
)做两条直线与⊙![]() 相切于
相切于![]() 两点,分别交抛物线于
两点,分别交抛物线于![]() 两点.
两点.
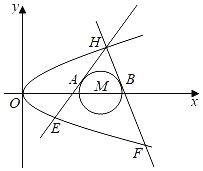
(1)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率;
的斜率;
(2)若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)﹣![]() ;(2)﹣11
;(2)﹣11
【解析】
(1)根据当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,可得点
轴时,可得点![]() 的坐标,因而
的坐标,因而![]() ,设
,设![]() ,由两点间斜率公式及抛物线方程代入化简可得
,由两点间斜率公式及抛物线方程代入化简可得![]() ,从而可求直线
,从而可求直线![]() 的斜率;
的斜率;
(2)设![]() ,由点斜式求出直线
,由点斜式求出直线![]() 、
、![]() 的方程,根据直线性质从而可得直线
的方程,根据直线性质从而可得直线![]() 的方程,令
的方程,令![]() ,可得
,可得![]() ,再利用导函数,即可求得
,再利用导函数,即可求得![]() 的最小值.
的最小值.
(1)抛物线![]() 和⊙
和⊙![]() :
:![]() ,则
,则![]() ,
,
∵当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,可知点
轴时,可知点![]() ,
,
且满足![]() ,设
,设![]() ,
,
∴由两点间斜率公式可得![]() ,
,
∴代入抛物线方程可知![]() ,即
,即![]() ,
,
∴![]() .
.
∴![]() .
.
(2)设![]() ,
,![]() ,抛物线
,抛物线![]() 和⊙
和⊙![]() :
:![]() ,则
,则![]() ,
,
∴由圆切线性质可知![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
同理可得直线![]() 的方程为
的方程为![]() ,
,
∴![]() ,
,![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
令![]() ,可得
,可得![]() ,(
,(![]() ),
),
∵![]() ,
,
∴![]() 关于
关于![]() 的函数在
的函数在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() .
.

【题目】我校随机抽取100名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 总计 | |
学习积极性高 | 40 | ||
学习积极性一般 | 30 | ||
总计 | 100 |
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法学生的学习积极性与对待班级工作的态度是否有关?并说明理由.附:
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
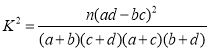
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |