题目内容
【题目】已知f（x）=x3+3ax2+bx+a2（a＞1）在x=﹣1时有极值0．
（1）求常数 a，b的值；
（2）方程f（x）=c在区间[﹣4，0]上有三个不同的实根时，求实数c的范围．
【答案】
（1）解：由f（x）=x3+3ax2+bx+a2，得：f′（x）=3x2+6ax+b
因为f（x）=x3+3ax2+bx+a2在x=﹣1时有极值O，
所以 
，即 
解得： 
或 
，
当a=1，b=3时，f（x）=x3+3x2+3x+1，
f′（x）=3x2+6x+3=3（x2+2x+1）=3（x+1）2≥0
所以函数f（x）=x3+3x2+3x+1在（﹣∞，+∞）上为增函数，
不满足在x=﹣1时有极值O，应舍掉，
所以，常数a，b的值分别为a=2，b=9
（2）解：当a=2，b=9时，f（x）=x3+6x2+9x+4，
f′（x）=3x2+12x+9，
由3x2+12x+9＞0，得：x＜﹣3或x＞﹣1，
由3x2+12x+9＜0，得：﹣3＜x＜﹣1．
所以，函数f（x）=x3+6x2+9x+4的增区间为（﹣∞，﹣3），（﹣1，+∞）．减区间为（﹣3，﹣1）．
又f（﹣4）=0，f（﹣3）=4，f（﹣1）=0，f（0）=4，
所以函数f（x）=x3+6x2+9x+4的大致图像如图，
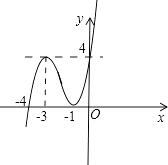
若方程f（x）=C在区间[﹣4，0]上有三个不同的实根，则函数y=f（x）与y=C的图像有三个不同的交点，
由图像可知方程f（x）=C在区间[﹣4，0]上有三个不同的实根时实数c的范围是（0，4）．
【解析】（1）求出函数f（x）的导函数，由f（x）=x3+3ax2+bx+a2在x=﹣1时有极值O，则f（﹣1）=0，f′（﹣1）=0，两式联立可求常数a，b的值；（2）把a，b代入后得到函数解析式，运用函数的导函数大于0和小于0求解函数f（x）的单调区间和函数f（x）的极值，再求出f（﹣4）和f（0），结合函数的单调性作出函数图像的大致形状，数形结合可求得实数c的范围．
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识，掌握求函数
的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧
,右侧
,那么
是极小值．
