Question

【题目】设x，y满足条件 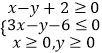，若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则 的最小值为（ ）
A.
B.
C.
D.4

Answer 1

【答案】D
【解析】解：不等式表示的平面区域如图所示阴影部分，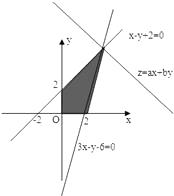
当直线ax+by=z（a＞0，b＞0）过直线x﹣y+2=0与直线3x﹣y﹣6=0的交点（4，6）时，目标函数z=ax+by（a＞0，b＞0）取得最大12，
∴4a+6b=12，即2a+3b=6，
∴ =（ ）× = （12+ ）≥4
当且仅当 时， 的最小值为4
故选D．
【考点精析】根据题目的已知条件，利用基本不等式和基本不等式在最值问题中的应用的相关知识可以得到问题的答案，需要掌握基本不等式：,（当且仅当时取到等号）；变形公式：；用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”．