题目内容
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C. | D.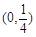 |
D
解析试题分析:∵抛物线方程为 ,∴
,∴ =1,∴
=1,∴ ,又∵焦点在
,又∵焦点在 轴的正半轴,∴焦点坐标为
轴的正半轴,∴焦点坐标为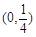 ,选D.
,选D.
考点:抛物线的标准方程.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
半径不等的两定圆 、
、 无公共点(
无公共点( 、
、 是两个不同的点),动圆
是两个不同的点),动圆 与圆
与圆 、
、 都内切,则圆心
都内切,则圆心 轨迹是( )
轨迹是( )
| A.双曲线的一支 | B.椭圆或圆 |
| C.双曲线的一支或椭圆或圆 | D.双曲线一支或椭圆 |
双曲线 的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是 ( )
的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是 ( )
| A.(-∞,0) | B.(1,+∞) |
| C.(-∞,0)∪(1,+∞) | D.(-∞,-1)∪(1,+∞) |
双曲线 的顶点和焦点到其渐近线距离的比是( )
的顶点和焦点到其渐近线距离的比是( )
A. | B. | C. | D.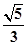 |
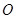 为坐标原点,
为坐标原点, 为抛物线
为抛物线 的焦点,
的焦点, 为
为 上一点,若
上一点,若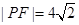 ,则
,则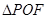 的面积为( )
的面积为( )
A. | B. | C. | D. |
已知双曲线C: -
- =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则C的渐近线方程为 ( )
,则C的渐近线方程为 ( )
A.y=± x x | B.y=± x x | C.y=± x x | D.y=±x |
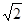 ,焦点到相应准线的距离为1,则该椭圆的离心率为( )
,焦点到相应准线的距离为1,则该椭圆的离心率为( )






 恒有公共点,则实数m的取值范围是( )
恒有公共点,则实数m的取值范围是( )


