题目内容
【题目】设函数f(x)=acos2x+(a﹣1)(cosx+1),其中a>0,记f(x)的最大值为A.
(1)求f′(x);
(2)求A;
(3)证明:|f′(x)|≤2A.
【答案】
(1)
解:f′(x)=﹣2asin2x﹣(a﹣1)sinx
(2)
当a≥1时,|f(x)|=|acos2x+(a﹣1)(cosx+1)|≤a+2(a﹣1)=3a﹣2=f(0),因此A=3a﹣2.
当0<a<1时,f(x)等价为f(x)=acos2x+(a﹣1)(cosx+1)=2acos2x+(a﹣1)cosx﹣1,
令g(t)=2at2+(a﹣1)t﹣1,
则A是|g(t)|在[﹣1,1]上的最大值,g(﹣1)=a,g(1)=3a﹣2,
且当t= ![]() 时,g(t)取得极小值,极小值为g(
时,g(t)取得极小值,极小值为g( ![]() )=﹣
)=﹣ ![]() ﹣1=﹣
﹣1=﹣ ![]() ,
,
令﹣1< ![]() <1,得a<
<1,得a< ![]() (舍)或a>
(舍)或a> ![]() .因此A=3a﹣2
.因此A=3a﹣2
g(﹣1)=a,g(1)=3a+2,a<3a+2,∴t=1时,g(t)取得最大值,g(1)=3a+2,即f(x)的最大值为3a+2.
综上可得:t=1时,g(t)取得最大值,g(1)=3a+2,即f(x)的最大值为3a+2.
∴A=3a+2.
①当0<a≤ ![]() 时,g(t)在(﹣1,1)内无极值点,|g(﹣1)|=a,|g(1)|=2﹣3a,|g(﹣1)|<|g(1)|,
时,g(t)在(﹣1,1)内无极值点,|g(﹣1)|=a,|g(1)|=2﹣3a,|g(﹣1)|<|g(1)|,
∴A=2﹣3a,
②当 ![]() <a<1时,由g(﹣1)﹣g(1)=2(1﹣a)>0,得g(﹣1)>g(1)>g(
<a<1时,由g(﹣1)﹣g(1)=2(1﹣a)>0,得g(﹣1)>g(1)>g( ![]() ),
),
又|g( ![]() )﹣g(﹣1)|=
)﹣g(﹣1)|= ![]() >0,
>0,
∴A=|g( ![]() )|=
)|= ![]() ,
,
综上,A= 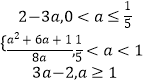 .
.
(3)
证明:由(1)可得:|f′(x)|=|﹣2asin2x﹣(a﹣1)sinx|≤2a+|a﹣1|,
当0<a≤ ![]() 时,|f′(x)|≤1+a≤2﹣4a<2(2﹣3a)=2A,
时,|f′(x)|≤1+a≤2﹣4a<2(2﹣3a)=2A,
当 ![]() <a<1时,A=
<a<1时,A= ![]() =
= ![]() +
+ ![]() +
+ ![]() ≥1,
≥1,
∴|f′(x)|≤1+a≤2A,
当a≥1时,|f′(x)|≤3a﹣1≤6a﹣4=2A,
综上:|f′(x)|≤2A.
【解析】(1)根据复合函数的导数公式进行求解即可求f′(x);
(2)讨论a的取值,利用分类讨论的数学,结合换元法,以及一元二次函数的最值的性质进行求解;
(3)由(1),结合绝对值不等式的性质即可证明:|f′(x)|≤2A.
本题主要考查函数的导数以及函数最值的应用,求函数的导数,利用函数单调性和导数的关系,以及换元法,转化法转化法转化为一元二次函数是解决本题的关键.综合性较强,难度较大.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |

