题目内容
7.给出下列等式:12=1
12+22=$\frac{1}{6}$×2×3×5
12+22+32=$\frac{1}{6}$×3×4×7
12+22+32+42=$\frac{1}{6}$×4×5×9
12+22+32+42+52=$\frac{1}{6}$×5×6×11
…
则按照此规律可以猜想第n个等式为12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$.
分析 根据题中式子各边的规律进行归纳猜想,即可得出第n个等式.
解答 解:12=1,
12+22=$\frac{1}{6}$×2×3×5,
12+22+32=$\frac{1}{6}$×3×4×7,
12+22+32+42=$\frac{1}{6}$×4×5×9,
12+22+32+42+52=$\frac{1}{6}$×5×6×11,…
由以上可得从第二个式子左边是连续数的平方和,右边分别是$\frac{1}{6}$与三个数的乘积,
且这三个数分别构成三个数列是:2、3、4、5、6…;3、4、5、6…;5、7、9、11…,
照此规律,第n个等式可为:12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$,
故答案为:12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$.
点评 本题考查归纳推理,难点是根据已知的几个式子的特点发现其中的规律,注意从运算的过程中去寻找,考查观察、分析、归纳的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.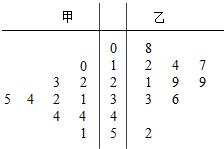 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知( )
 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知( )| A. | 甲运动员的最低得分为0分 | |
| B. | 乙运动员得分的中位数是29 | |
| C. | 甲运动员得分的众数为44 | |
| D. | 乙运动员得分的平均值在区间(11,19)内 |
2.等比数列{an}中,a1+a2=40,a3+a4=60,那么a7+a8=( )
| A. | 9 | B. | 100 | C. | 135 | D. | 80 |
16.将正奇数1,3,5,7,…按如表的方式进行排列,记aij表示第i行第j列的数,若aij=2015,则i+j的值为( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 1 | 3 | 5 | 7 | |
| 第2行 | 15 | 13 | 11 | 9 | |
| 第3行 | 17 | 19 | 21 | 23 | |
| 第4行 | 31 | 29 | 27 | 25 | |
| 第5行 | 39 | 37 | 35 | 33 | |
| … | … | … | … | … | … |
| A. | 505 | B. | 506 | C. | 254 | D. | 253 |