题目内容
【题目】在平面直角坐标系xOy中，已知椭圆C1： 
（a＞b＞0）的左焦点为F1（﹣1，0），且点P（0，1）在C1上．
（1）求椭圆C1的方程；
（2）设直线l同时与椭圆C1和抛物线C2：y2=4x相切，求直线l的方程．
【答案】
（1）解：因为椭圆C1的左焦点为F1（﹣1，0），所以c=1，
点P（0，1）代入椭圆 
，得 
，即b=1，
所以a2=b2+c2=2
所以椭圆C1的方程为 
（2）解：直线l的斜率显然存在，
设直线l的方程为y=kx+m，
由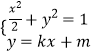 
，消去y并整理得（1+2k2）x2+4kmx+2m2﹣2=0，
因为直线l与椭圆C1相切，
所以△=16k2m2﹣4（1+2k2）（2m2﹣2）=0
整理得2k2﹣m2+1=0①
由 
，消去y并整理得k2x2+（2km﹣4）x+m2=0
因为直线l与抛物线C2相切，所以△=（2km﹣4）2﹣4k2m2=0
整理得km=1②
综合①②，解得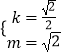 
或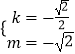 
所以直线l的方程为 
或 
【解析】（1）因为椭圆C1的左焦点为F1（﹣1，0），所以c=1，点P（0，1）代入椭圆 ，得b=1，由此能求出椭圆C1的方程．（2）设直线l的方程为y=kx+m，由 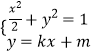，得（1+2k2）x2+4kmx+2m2﹣2=0．因为直线l与椭圆C1相切，所以△=16k2m2﹣4（1+2k2）（2m2﹣2）=0．由此能求出直线l的方程．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
练习册系列答案
相关题目
