题目内容
已知△ABC的面积S满足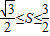 ,且
,且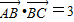 ,
, 与
与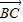 的夹角为θ.
的夹角为θ.(1)求θ的取值范围;
(2)求函数
 的最大值及最小值.
的最大值及最小值.
【答案】分析:(1)由条件求得 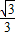 ≤tanθ≤1,再根据0≤θ≤π,从而求出θ的取值范围.
≤tanθ≤1,再根据0≤θ≤π,从而求出θ的取值范围.
(2)利用两角和差的正弦公式、二倍角公式花简函数f(θ)的解析式为2sin(2θ-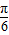 )+2,根据
)+2,根据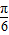 ≤θ≤
≤θ≤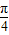 ,求得2θ-
,求得2θ-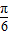 的范围,从而求得sin(2θ-
的范围,从而求得sin(2θ-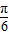 )的范围,从而求出f(θ)的最大值和最小值.
)的范围,从而求出f(θ)的最大值和最小值.
解答:解:(1)因为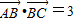 ,
,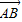 与
与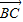 的夹角为θ,所以,
的夹角为θ,所以,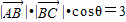 .
.
S=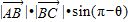 =
=
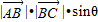 . (3分)
. (3分)
又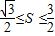 ,所以,
,所以,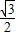 ≤
≤ •tanθ≤
•tanθ≤ ,即
,即 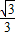 ≤tanθ≤1,
≤tanθ≤1,
又0≤θ≤π,所以,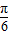 ≤θ≤
≤θ≤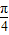 . (6分)
. (6分)
(2)函数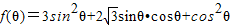 =2sin2θ+
=2sin2θ+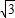 sin2θ+1
sin2θ+1
=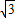 sin2θ-cos2θ+2=2sin(2θ-
sin2θ-cos2θ+2=2sin(2θ-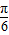 )+2,----(9分)
)+2,----(9分)
因为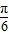 ≤θ≤
≤θ≤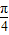 ,所以
,所以 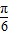 ≤2θ-
≤2θ-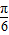 ≤
≤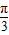 ,(10分)
,(10分)
从而当 θ=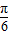 时,f(θ)取得最小值为3,
时,f(θ)取得最小值为3,
当 θ=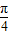 时,f(θ)取得最大值为
时,f(θ)取得最大值为 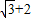 .---------(12分)
.---------(12分)
点评:本题主要考查两个向量的数量积的运算,正弦函数的定义域和值域,两角和差的正弦公式、二倍角公式的应用,属于中档题.
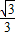 ≤tanθ≤1,再根据0≤θ≤π,从而求出θ的取值范围.
≤tanθ≤1,再根据0≤θ≤π,从而求出θ的取值范围.(2)利用两角和差的正弦公式、二倍角公式花简函数f(θ)的解析式为2sin(2θ-
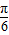 )+2,根据
)+2,根据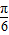 ≤θ≤
≤θ≤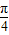 ,求得2θ-
,求得2θ-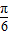 的范围,从而求得sin(2θ-
的范围,从而求得sin(2θ-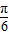 )的范围,从而求出f(θ)的最大值和最小值.
)的范围,从而求出f(θ)的最大值和最小值.解答:解:(1)因为
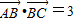 ,
,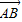 与
与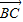 的夹角为θ,所以,
的夹角为θ,所以,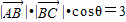 .
.S=
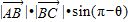 =
=
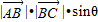 . (3分)
. (3分)又
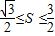 ,所以,
,所以,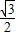 ≤
≤ •tanθ≤
•tanθ≤ ,即
,即 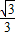 ≤tanθ≤1,
≤tanθ≤1,又0≤θ≤π,所以,
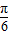 ≤θ≤
≤θ≤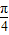 . (6分)
. (6分)(2)函数
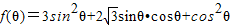 =2sin2θ+
=2sin2θ+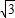 sin2θ+1
sin2θ+1=
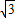 sin2θ-cos2θ+2=2sin(2θ-
sin2θ-cos2θ+2=2sin(2θ-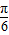 )+2,----(9分)
)+2,----(9分)因为
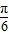 ≤θ≤
≤θ≤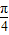 ,所以
,所以 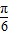 ≤2θ-
≤2θ-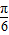 ≤
≤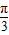 ,(10分)
,(10分)从而当 θ=
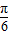 时,f(θ)取得最小值为3,
时,f(θ)取得最小值为3,当 θ=
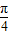 时,f(θ)取得最大值为
时,f(θ)取得最大值为 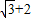 .---------(12分)
.---------(12分)点评:本题主要考查两个向量的数量积的运算,正弦函数的定义域和值域,两角和差的正弦公式、二倍角公式的应用,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目