题目内容
20.已知函数f(x)=x2+mx+m+1(m>5)的两个零点分别为tanα,tanβ,且α,β∈(-$\frac{π}{2}$,$\frac{π}{2}$),则α+β的值为( )| A. | $\frac{π}{4}$ | B. | -$\frac{π}{4}$ | C. | $\frac{3}{4}π$ | D. | -$\frac{3}{4}π$ |
分析 由条件利用韦达定理可得tanα+tanβ=-m<-5,tanα•tanβ=m+1>6,α、β∈(-$\frac{π}{2}$,0),α+β∈(-π,0).再根据 tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$ 的值,求得α+β 的值.
解答 解:由题意可得m>5,tanα+tanβ=-m<-5,tanα•tanβ=m+1>6,α,β∈(-$\frac{π}{2}$,$\frac{π}{2}$),
∴α、β∈(-$\frac{π}{2}$,0),α+β∈(-π,0).
再根据 tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1,可得α+β=-$\frac{3π}{4}$,
故选:D.
点评 本题主要考查韦达定理、两角和的正切公式,根据三角函数的值求角,属于基础题.

练习册系列答案
相关题目
11.函数y=log2x+log22(2x2)的值域是( )
| A. | (-∞,0] | B. | [4,+∞) | C. | [0,4] | D. | [-$\frac{9}{16}$,+∞) |
15.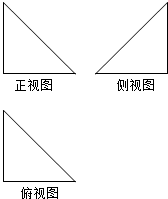 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )| A. | $\frac{18+9\sqrt{3}}{2}$ | B. | 18+9$\sqrt{3}$ | C. | 3 | D. | 9 |
11.指数函数f(x)=ax(a>0,a≠1)的图象经过点(2,16),则实数a的值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
 如图,以第 ①个等腰直角三角形的斜边作为第 ②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边作为第 ③个等腰直角三角形的腰,依此类推,若第 ⑨个等腰直角三角形的斜边长为$16\sqrt{3}$厘米,则第 ①个等腰直角三角形的斜边长为$\sqrt{3}$厘米.
如图,以第 ①个等腰直角三角形的斜边作为第 ②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边作为第 ③个等腰直角三角形的腰,依此类推,若第 ⑨个等腰直角三角形的斜边长为$16\sqrt{3}$厘米,则第 ①个等腰直角三角形的斜边长为$\sqrt{3}$厘米.