题目内容
顶点在同一球面上的正四棱柱体ABCD-A1B1C1D1中, ,
, ,则
,则 两点间的球面距离为 ( )
两点间的球面距离为 ( )
A. | B. | C. | D. |
B
解析试题分析:已知正四棱柱ABCD-A1B1C1D1的底面ABCD边长为1,高 ,它的八个顶点都在同一球面上,那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.
,它的八个顶点都在同一球面上,那么,正四棱柱ABCD-A1B1C1D1的对角线长为球的直径,中点O为球心.
正四棱柱对角线AC1=2,则球的半径为1.
根据题中所给数据,可得∠AOC= ,则A,C两点的球面距离为
,则A,C两点的球面距离为 。选B.
。选B.
考点:正四棱柱及其外接球的几何特征,球面距离的概念。
点评:简单题,关键是认识到:正四棱柱ABCD-A1B1C1D1的八个顶点都在同一球面上,得到正四棱柱ABCD-A1B1C1D1的对角线长即为球的直径。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一只蚂蚁从正方体 的顶点
的顶点 处出发,经正方体的表面,按最短路线爬行到达顶点
处出发,经正方体的表面,按最短路线爬行到达顶点 位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是
位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是
| A.①② | B.①③ | C.②④ | D.③④ |
四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系正确的是( )
| A.h2>h1>h4 | B.h1>h2>h3 | C.h3>h2>h4 | D.h2>h4>h1 |
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
A.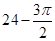 | B. | C. | D. |





 ,则这个圆锥的全面积是( )
,则这个圆锥的全面积是( )












 三点,其中点
三点,其中点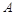 与
与 两点间的球面距离均为
两点间的球面距离均为 ,
, ,则球心到平面
,则球心到平面 的距离为( )
的距离为( )